Контактные данные

Решение задач ТОЭ

Вконтакте

Решение ТОЭ онлайн

Главная → Примеры решения задач ТОЭ → Электроемкость. Емкость конденсатора

Электроемкость. Емкость конденсатора

Электроемкость. Емкость конденсатора

Основные положения и соотношения

1. Закон Кулона

$F = \frac{Q_{1} \cdot Q_{2}}{4 π \cdot ε_{a} \cdot R^{2}},$ (1)

здесь

F — сила взаимодействия между зарядами;

Q₁ и Q₂ — точечные заряды;

R — расстояние между ними;

ε_a — абсолютная диэлектрическая проницаемость среды, равная ε₀·ε_r;

ε_r — относительная диэлектрическая проницаемость;

ε_{0} = \frac{1}{4 π \cdot с^{2} \cdot 10^{- 7}} \approx 8,85418782 \cdot 10^{- 12} \frac{Ф}{м}

– электрическая постоянная.

2. Напряженность электростатического поля точечного заряда Q на расстоянии R от него

$E = \frac{Q}{4 π \cdot ε_{a} \cdot R^{2}} .$ (2)

Напряженность поля в любой точке между пластинами плоского конденсатора вдалеке от краев

$E = \frac{U}{d},$ (3)

здесь d — расстояние между пластинами конденсатора, U — напряжение.

Напряженность поля в точке, отстоящей на расстоянии r от бесконечно длинной заряженной оси с линейной плотностью τ

$E = \frac{τ}{2 π \cdot ε_{a} \cdot r} .$ (4)

Напряженность поля в точке, отстоящей на расстоянии r от оси цилиндрического конденсатора (r₁ <r < r₂)

$E = \frac{U}{r \cdot \ln \frac{r_{2}}{r_{1}}},$ (5)

здесь U — напряжение конденсатора, r₁ и r₂ — соответственно внутренний и внешний радиусы конденсатора.

Напряженность поля в точке, отстоящей на расстоянии R от центра сферического конденсатора (R₁ < R < R₂)

$E = \frac{U \cdot R_{1} \cdot R_{2}}{R^{2} \cdot (R_{2} - R_{1})},$ (6)

здесь U — напряжение конденсатора, R₁ и R₂ — соответственно внутренний и внешний радиусы конденсатора.

3. Вектор электрического смещения

$\vec{D} = ε_{a} \cdot \vec{E} .$ (7)

4. Общее выражение емкости конденсатора

$C = \frac{Q}{U} .$ (8)

Емкость плоского конденсатора

$C = \frac{ε_{a} \cdot S}{d} = \frac{ε_{r} \cdot ε_{0} \cdot S}{d},$ (9)

здесь S — поверхность каждой пластины конденсатора; d — расстояние между ними.
Скачать статью Вывод формулы емкости плоского конденсатора

Емкость цилиндрического конденсатора

$C = \frac{2 π \cdot ε_{a} \cdot l}{\ln \frac{r_{2}}{r_{1}}},$ (10)

здесь l — длина конденсатора, r₁ и r₂ — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости коаксиального кабеля

Емкость сферического конденсатора

$C = \frac{4 π \cdot ε_{a} \cdot R_{1} \cdot R_{2}}{R_{2} - R_{1}},$ (11)

здесь R₁ и R₂ — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости сферического конденсатора

Емкость двухпроводной линии

$C = \frac{π \cdot ε_{a} \cdot l}{\ln [\frac{D}{2 a} + \sqrt{{(\frac{D}{2 a})}^{2} - 1}]},$ (12)

здесь l — длина линии, D — расстояние между осями проводов, a — радиус проводов.

Емкость однопроводной линии

$C = \frac{2 π \cdot ε_{a} \cdot l}{\ln [\frac{h}{a} + \sqrt{{(\frac{h}{a})}^{2} - 1}]},$ (13)

здесь l — длина линии, h — высота подвеса провода над землей, a — радиус провода.

5. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

$C = C_{1} + C_{2} + … + C_{n} = \sum_{k = 1}^{n} C_{k} .$ (14)

При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

$\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + … + \frac{1}{C_{n}} = \sum_{k = 1}^{n} \frac{1}{C_{k}} .$ (15)

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет

$C = \frac{C_{1} \cdot C_{2}}{C_{1} + C_{2}},$ (16)

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям

$U_{1} = U \cdot \frac{C_{2}}{C_{1} + C_{2}}; U_{2} = U \cdot \frac{C_{1}}{C_{1} + C_{2}} .$ (17)

6. Энергия электростатического поля конденсатора

$W = \frac{C \cdot U^{2}}{2} = \frac{Q \cdot U}{2} = \frac{Q^{2}}{2 C} .$ (18)

Удельная энергия электростатического поля (на единицу объема диэлектрика) выражается следующим образом

$w = \frac{d W}{d V} = \frac{E \cdot D}{2} = \frac{ε_{a} \cdot E^{2}}{2} .$ (19)

Общая величина энергии электростатического поля выражается интегралом величины удельной энергии по всему объему диэлектрика конденсатора

$W = \int_{V} \frac{ε_{a} \cdot E^{2}}{2} d V .$ (20)

7. Расчет распределения зарядов в сложных цепях, содержащих источники э. д. с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

$Σ Q = Σ Q^{'} .$ (21)

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

$\sum_{k = 1}^{n} E_{k} = \sum_{k = 1}^{n} U_{C k} = \sum_{k = 1}^{n} \frac{Q_{k}}{C_{k}} .$ (22)

Упражнения и задачи

Задача 1. Имеется конденсатор переменной емкости от 500 до 1500 пФ. Указать, какой добавочный конденсатор с минимальным диапазоном переменной емкости следует взять и как его включить, чтобы эквивалентная емкость изменялась от 100 до 250 пФ.

Ответ: 125 — 300 пФ, включить параллельно.

Где можно купить памятник.

Задача 2. Емкость плоского конденсатора, имеющего слюдяной диэлектрик, равна 44,3 пФ. Площадь каждой пластины конденсатора составляет 25 см², расстояние между пластинами равно 3 мм.

Чему равна относительная диэлектрическая проницаемость слюды? Принимая пробивное напряжение слюды равным 80 кВ/мм, определить, при каком максимальном напряжении может работать этот конденсатор, чтобы он имел трехкратный запас прочности.

Начертить график изменения потенциала между пластинами конденсатора.

Ответ: ε_r = 6; U_max = 80 кВ; график падения потенциала вычерчивается по уравнению φ = U·(1 — x/d), здесь U — потенциал положительно заряженной обкладки, принятый равным напряжению конденсатора, d — расстояние между пластинами, x — переменное расстояние до положительной обкладки конденсатора.

Задача 3. Доказать, что многопластинчатый конденсатор (рис. 1), состоящий из n одинаковых пластин, площадью S каждая, с рас стоянием между двумя соседними пластинами d, с диэлектриком, абсолютная диэлектрическая проницаемость которого ε, имеет емкость, равную

$C = \frac{ε_{a} \cdot S \cdot (n - 1)}{d} .$

Многопластинчатый конденсатор

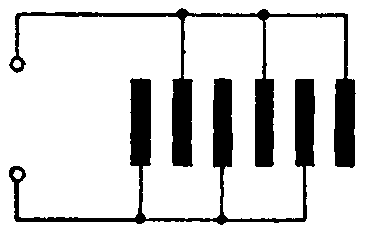
Рис. 1

Подсчитать, сколько надо взять листов станиоля, каждый площадью S = 40 см², чтобы получить многопластинчатый конденсатор емкостью 0,5 мкФ при условии, что диэлектриком является парафинированная бумага (ε_r = 1,8) толщиною 0,05 мм.

Ответ: 393 листа.

Задача 4. Плоский слоистый конденсатор (рис. 2), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщиною d₁ = 0,3 мм и стекла (ε_r₂ = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Емкость плоского двухслойного конденсатора

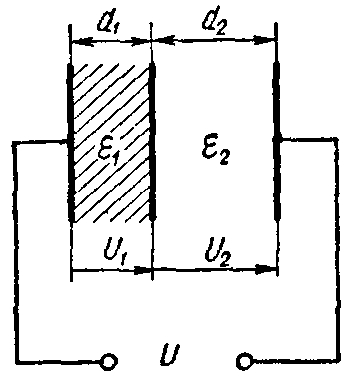
Рис. 2

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

$C = \frac{C_{1} \cdot C_{2}}{C_{1} + C_{2}} = \frac{\frac{ε_{a 1} \cdot S}{d_{1}} \cdot \frac{ε_{a 2} \cdot S}{d_{2}}}{\frac{ε_{a 1} \cdot S}{d_{1}} + \frac{ε_{a 2} \cdot S}{d_{2}}} = \frac{ε_{a 1} \cdot ε_{a 2} \cdot S}{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}} .$

Подставляя сюда числовые значения, предварительно заменив ε_a₁ = ε₀ε_r₁ и ε_a₂ = ε₀ε_r₂, получим

$C = \frac{ε_{0} \cdot ε_{r 1} \cdot ε_{r 2} \cdot S}{ε_{r 1} \cdot d_{2} + ε_{r 2} \cdot d_{1}} = 8,85 \cdot 10^{- 12} \cdot \frac{6 \cdot 7 \cdot 12 \cdot 10^{- 4}}{6 \cdot 0,4 \cdot 10^{- 3} + 7 \cdot 0,3 \cdot 10^{- 3}} = 99 \cdot 10^{- 12} Ф .$

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

$\begin{array}{l} U_{1} = \frac{Q}{C_{1}} = \frac{C \cdot U_{п р}}{\frac{ε_{a 1} \cdot S}{d_{1}}} = \frac{ε_{a 2} \cdot d_{1}}{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}} \cdot U_{п р}; \\ U_{2} = \frac{Q}{C_{2}} = \frac{C \cdot U_{п р}}{\frac{ε_{a 2} \cdot S}{d_{2}}} = \frac{ε_{a 1} \cdot d_{2}}{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}} \cdot U_{п р} . \end{array}$

Напряженности электростатического поля в каждом слое

$\begin{array}{l} E_{1} = \frac{U_{1}}{d_{1}} = \frac{ε_{a 2}}{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}} \cdot {U^{'}}_{п р}; \\ E_{2} = \frac{U_{2}}{d_{2}} = \frac{ε_{a 1}}{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}} \cdot {U^{″}}_{п р} . \end{array}$

Здесь U'_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U''_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

$\begin{array}{l} {U^{'}}_{п р} = E_{1} \cdot \frac{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}}{ε_{a 2}} = 49,5 к В; \\ {U^{″}}_{п р} = E_{2} \cdot \frac{ε_{a 1} \cdot d_{2} + ε_{a 2} \cdot d_{1}}{ε_{a 1}} = 27,0 к В . \end{array}$

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 5. Вычислить емкость 1 км коаксиального кабеля типа 2,6/9,4. В этом кабеле изоляция осуществлена с помощью полиэтиленовых шайб (ε_r = 2,2) толщиною a = 2,2 мм, размещенных через равные промежутки b = 25 мм, остальное пространство между шайбами заполнено воздухом (рис. 3). Диаметр жилы d = 2,6 мм, внутренний диаметр наружного провода D = 9,4 мм.

Емкость коаксиального кабеля с изоляцией из полиэтиленовых шайб

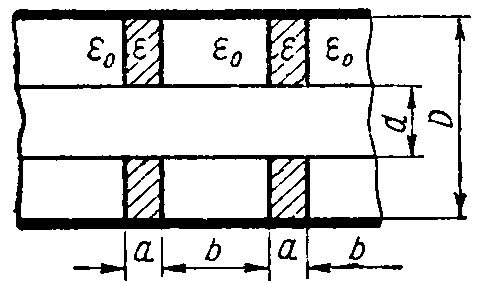
Рис. 3

Указание. Емкость кабеля может быть подсчитана, исходя из того, что отдельные его участки соединены параллельно.

Ответ: 48·10^–9 Ф/км = 48 нФ/км.

Задача 6. Силовой одножильный кабель с резиновой изоляцией в свинцовой оболочке марки СРГ имеет сечение жилы 25 мм². Известно, что наибольшая напряженность электростатического поля в изоляции кабеля не должна превышать 6 кВ/мм. Определить толщину слоя резиновой изоляции, если при испытании кабеля между жилой и оболочкой включают напряжение, равное 10 кВ.

Принимая потенциал жилы кабеля равным U = 10 кВ, построить график падения потенциала в диэлектрике кабеля в зависимости от расстояния до центра кабеля.

Ответ: 2,25 мм. График строится по уравнению $φ (r) = \frac{U \cdot \ln \frac{r_{2}}{r}}{\ln \frac{r_{2}}{r_{1}}} .$

Задача 7. Цилиндрический конденсатор длиною l = 5 см имеет двухслойный диэлектрик (рис. 4).

Емкость двухслойного цилиндрического конденсатора

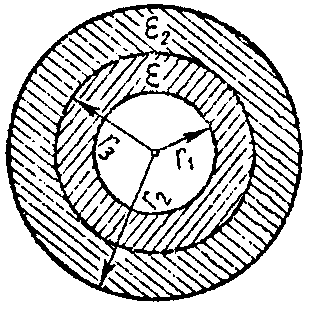
Рис. 4

Внутренний радиус r₁ = 1 см, внешний — r₂ = 3 см, радиус разграничения слоев диэлектриков r₃ = 1.5 см. Относительные диэлектрические проницаемости: внутреннего слоя изоляции ε_r₁ = 2, наружного ε_r₂ = 4.

Вычислить емкость конденсатора и начертить кривые изменения напряженностей и потенциалов в каждом из слоев, если конденсатор находится под напряжением U = 2 кВ.

Указание. При помощи теоремы Гаусса находятся напряженности электростатического поля в каждом из слоев

$E_{1} = \frac{τ}{2 π \cdot ε_{a 1} \cdot r}; E_{2} = \frac{τ}{2 π \cdot ε_{a 2} \cdot r},$

где τ — линейная плотность заряда (заряд на единицу длины конденсатора). Затем вычисляется напряжение между обкладками конденсатора по формуле

$U = \int_{r_{1}}^{r_{3}} E_{1} d r + \int_{r_{3}}^{r_{2}} E_{2} d r .$

Отсюда определяется линейная плотность заряда

$τ = \frac{2 π \cdot U}{\frac{1}{ε_{a 1}} \ln \frac{r_{3}}{r_{1}} + \frac{1}{ε_{a 2}} \ln \frac{r_{2}}{r_{3}}} .$

Емкость конденсатора вычисляется по формуле (8). Потенциал φ₁ в любой точке области первого слоя диэлектрика (r₃ > r > r₁) определяется из выражения

$φ_{r_{1}} - φ_{1} = \int_{r_{1}}^{r} E_{1} d r,$

а потенциал φ₂ в любой точке области второго слоя (r₂ > r > r₃) диэлектрика вычисляется из выражения

$φ_{r_{2}} - φ_{2} = \int_{r_{2}}^{r} E_{2} d r .$

В последних формулах φ_r₁ = U — потенциал внутренней обкладки конденсатора, φ_r₂ — потенциал на границе раздела диэлектриков. Внешняя оболочка заземлена: φ₂(r₂) = 0.

Ответ:

$\begin{array}{l} C = \frac{2 π \cdot l}{\frac{1}{ε_{a 1}} \ln \frac{r_{3}}{r_{1}} + \frac{1}{ε_{a 2}} \ln \frac{r_{2}}{r_{3}}}; \\ E_{1} (r) = \frac{U}{r \cdot (\ln \frac{r_{3}}{r_{1}} + \frac{ε_{a 1}}{ε_{a 2}} \ln \frac{r_{2}}{r_{3}})}; E_{2} (r) = \frac{U}{r \cdot (\frac{ε_{a 2}}{ε_{a 1}} \ln \frac{r_{3}}{r_{1}} + \ln \frac{r_{2}}{r_{3}})}; \\ φ_{1} (r) = U \cdot (1 - \frac{\ln \frac{r}{r_{1}}}{\ln \frac{r_{3}}{r_{1}} + \frac{ε_{a 1}}{ε_{a 2}} \ln \frac{r_{2}}{r_{3}}}); φ_{2} (r) = \frac{U \cdot \frac{ε_{a 1}}{ε_{a 2}} \ln \frac{r_{2}}{r}}{\ln \frac{r_{3}}{r_{1}} + \frac{ε_{a 1}}{ε_{a 2}} \ln \frac{r_{2}}{r_{3}}} . \end{array}$

Пример вывода формулы емкости двухслойного цилиндрического конденсатора при помощи теоремы Гаусса

Знакомства в Ханты Мансийске - необычайная возможность познакомиться с интересными девушками в https://hm.intim-gid.com и добавить новые главы в свою любовную историю. Отправляйтесь на увлекательные свидания с привлекательными девушками из Керчи, найденными на https://kerch.intim-gid.com, и создайте свой собственный роман. Познакомьтесь с прекрасными девушками Салавата на https://salavat.feixxx.net и откройте новую главу в своей личной жизни!. Учитесь читать между строками сердец прекрасных девушек Тулы на сайте знакомств https://tula.feixxx.net и переводите э. Встречайтесь с прекрасными девушками в Златоусте - https://zlat.intim-gid.com поможет вам найти идеальную половинку!. Возможность встретиться с добрыми и чувственными девушками в Томске предоставлена на сайте https://tomsksm.com. Жаждете романтики? У нас есть множество прекрасных девушек, которые хотят общения – https://vdonsk.feixxx.net. Отправляйся на поле знакомств с https://vlg.feixxx.net, чтобы найти свою вторую половинку. Запоминающиеся эмоции и нежные прикосновения ждут вас на сайте https://kalugasm.com.

Задача 8. Чему равен внешний радиус сферического конденсатора емкостью 20 пФ, внутренний радиус которого 2 см. а относительная Диэлектрическая проницаемость изоляции ε_r = 3. При каком напряжении конденсатор будет пробит, если пробивное напряжение изоляции равно 15 кВ/мм?

Ответ: 3 см, 100 кВ.

Задача 9. Найти емкость сферического конденсатора, изображенного на рис. 5.

Емкость сферического конденсатора

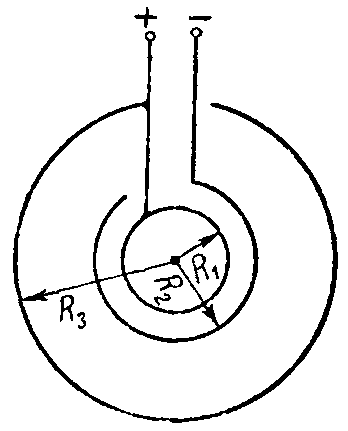
Рис. 5

Даны радиусы R₁, R₂ и R₃; изоляция однородная, ее абсолютная диэлектрическая проницаемость равна ε.

Указание. Данный конденсатор может быть рассмотрен как два Параллельно соединенных конденсатора.

Ответ: $C = \frac{4 π \cdot ε_{a} \cdot R_{2}^{2} \cdot (R_{3} - R_{1})}{(R_{3} - R_{2}) (R_{2} - R_{1})} .$

Задача 10. К пластинам плоского двухслойного конденсатора приложено напряжение 3 кВ. Площадь пластины равна 5 см². Толщины первого и второго слоев конденсатора равны соответственно 4 и 6 мм, а диэлектрические проницаемости — 6 и 1.

Построить графики изменения напряженности и потенциала между пластинами в зависимости от расстояния до положительной пластины, потенциал которой принять равным + 3 кв.

Задача 11. Имеется два одинаковых конденсатора переменной емкости. Емкость каждого конденсатора можно плавно изменять от 20 до 200 пФ.

Какие границы изменения емкости можно получить при различном соединении этих конденсаторов между собой?

Ответ: от 10 до 400 пФ.

Задача 12. Определить емкость воздушной двухпроводной линии длиной 2 км, если диаметр проводов равен 3 мм и расстояние между осями проводов составляет 30 см.

Задача 13. Определить емкость однопроводной телеграфной линии длиною 180 км, если диаметр провода равен 3 мм, а средняя высота подвеса провода над землей составляет 7 м.

Начертить кривую зависимости емкости этого провода в функции расстояния от земли.

Ответ: 1,1 мкФ.

Задача 14. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

$W_{1} = \frac{C_{1} \cdot U^{2}}{2} = \frac{ε_{0} \cdot S}{d_{1}} \cdot \frac{U^{2}}{2},$

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как $C_{2} = \frac{ε_{0} \cdot S}{d_{2}}$ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

$W_{2} = \frac{ε_{0} \cdot S}{d_{2}} \cdot \frac{U_{2}^{2}}{2} = \frac{ε_{0} \cdot S}{10 d_{1}} \cdot \frac{{(10 U)}^{2}}{2} = 10 \cdot \frac{ε_{0} \cdot S}{d_{1}} \cdot \frac{U^{2}}{2} = 10 \cdot W_{1} .$

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

$W_{2} - W_{1} = 9 \cdot W_{1} = 9 \cdot \frac{ε_{0} \cdot S}{d_{1}} \cdot \frac{U^{2}}{2} = 2,86 \cdot 10^{- 7} Д ж .$

Задача 15. Плоский конденсатор с воздушным диэлектриком заряжается от источника электрической энергии с напряжением U.

Определить, как изменится энергия конденсатора, если после отключения его от источника энергии расстояние между обкладками увеличить вдвое.

Ответ: энергия увеличится в два раза.

Задача 16. Плоский конденсатор с диэлектриком из эбонита (ε_r = 2,5) в виде пластинки толщиной d = 5 см присоединен к полюсам батареи. После зарядки эбонитовая пластинка вынимается. Как нужно изменить расстояние между обкладками конденсатора, чтобы энергия конденсатора осталась без изменения?

Задачу решить в двух случаях: 1) если конденсатор остается присоединенным к батарее и 2) если конденсатор отключить от батареи.

Ответ: в обоих случаях пластины должны отстоять друг от друга на расстоянии 2 см.

Задача 17. Конденсатор емкостью C₁ = 40 мкФ заряжен от сети до напряжения U₁ = 220 В; другой конденсатор емкостью C₂ = 10 мкФ заряжен от другой сети до напряжения U₂ = 110 В.

Положительные зажимы конденсаторов после отсоединения от источников соединяются вместе:

а) Чему равна разность потенциалов между отрицательными зажимами конденсаторов?

б) Чему равны заряды до и после последующего соединения друг с другом отрицательных зажимов конденсаторов?

в) Чему равны напряжения на конденсаторах после соединения их отрицательных зажимов?

г) Чему равна энергия каждого конденсатора до. и после соединения отрицательных зажимов?

Ответ: а) 110 В, б) до соединения: Q₁ = 8800 мкКл, Q₂ = 1100 мкКл; после соединения: Q′₁ = 7920 мкКл, Q′₂ = 1980 мкКл, в) 198 В, г) до соединения: W₁ = 0,97 Дж, W₂ = 0,06 Дж; после соединения: W′₁ = 0,784 Дж, W′₂ = 0,196 Дж.

Задача 18. Три последовательно соединенных конденсатора, емкости которых 2, 10 и 15 мкФ, заряжаются от сети с напряжением 120 В. После отключения от сети конденсаторы разъединяются друг от друга без потери заряда. Если затем конденсаторы соединить параллельно, то чему будет равно напряжение на их зажимах?

Ответ: 20 В.

Список литературы

1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. — М.: Гардарики, 2001.– 317 с.

2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: в 3-х тт.: Учебник для вузов. Том 3. –4-е изд. — СПб.: Питер, 2003. — 377 с.

3. Купалян С.Д. Теоретические основы электротехники / Под ред. Г.И. Атабекова. — М.-Л.: Госэнергоиздат, 1963. — ч. 3. Электромагнитное поле. — 112 с.

4. Теоретические основы электротехники. т. 2. Нелинейные цепи и основы теории электромагнитного поля. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. — М.: Высш. шк., 1976. — 383 с.

5. Поливанов, К.М. Теоретические основы электротехники: в 3-х ч. / К.М. Поливанов. ч. 3: Теория электромагнитного поля. — М.: Энергия, 1969. — 352 с.

6. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов / Бессонов Л.А., Демидова И.Г. и др.; Под ред. Л.А. Бессонова. — М., Высшая школа, 2000. — 528с.: ил.

7. Колли Я.Н. и др. Задачник по теоретическим основам электротехники (теория поля). Уч. пособие для вузов. Под ред. Поливанова К.М. — М., «Энергия», 1972.

8. Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие. — М., Энергоиздат, 1982. — 768с.

9. Татур Т.А. Основы теории электромагнитного поля: Справочное пособие. — М.: Высш. шк., 1989 . — 270 с.

электрическая постоянная, емкость конденсатора, электроемкость, емкость плоского конденсатора, емкость цилиндрического конденсатора, сферический конденсатор, емкость двухпроводной линии, емкость однопроводной линии, емкость коаксиального кабеля

Заказать решение ТОЭ

Новости

Контактные данные

Электроемкость. Емкость конденсатора

Метки