4.2 Примеры расчета схем при несинусоидальных периодических воздействиях
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 4 Анализ схем при несинусоидальных периодических воздействияхПримеры расчета схем при несинусоидальных периодических воздействиях
Задача 4.1 К генератору с несинусоидальным периодическим напряжением подключена цепь, состоящая из последовательного соединения активного сопротивления, индуктивности и емкости.
Написать уравнение тока в цепи, если напряжение генератора может быть выражено уравнением
Найти действующее значение напряжения на конденсаторе и мощность, расходуемую в цепи, где R = 50 Ом, L = 0,05 Гн, C = 5 мкФ.
Решение В последовательном соединении имеется конденсатор, поэтому ток постоянной составляющей содержать не будет! Амплитуды гармонических составляющих определяются по формуле
где
Фазовый сдвиг гармоники тока относительно соответствующего напряжения из треугольника сопротивлений
Напряжение на конденсаторе дается выражением
Уравнение тока в цепи имеет вид
Расчет дает следующие значения
UC = 143 В; P = 51,8 Вт.
Задача 4.2 На вход схемы (рис. 4.1)
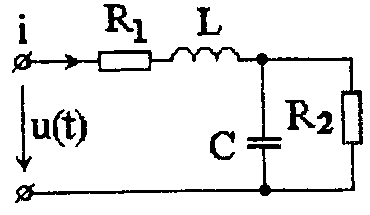
Рис. 4.1 На вход схемы подано напряжение от идеального двухполупериодного выпрямителя
с параметрами R1 = 100 Ом, R2 = 600 Ом, ωL = 3000 Ом; 1/(ωC) = 20 Ом подано напряжение от идеального двухполупериодного выпрямителя с частотой ω (рис. 4.2).
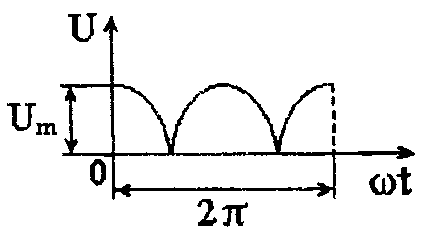
Рис. 4.2 Напряжение от идеального двухполупериодного выпрямителя
Найти входной ток i(t).Вычислить для переменной составляющей приложенного напряжения коэффициенты формы, искажения, амплитуды.
Решение Ряд Фурье исходного напряжения находим по справочной литературе. Ограничимся четырьмя гармониками
Постоянная составляющая
Гармонические составляющие изменяются по косинусоидальному закону с нулевой фазой
Входное комплексное сопротивление k-ой гармоники Z(k) определяется из выражения
Определим составляющие входного тока.
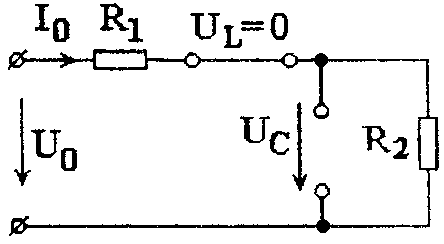
Рис. 4.3 Схема замещения цепи для определения постоянной составляющей тока
Постоянная составляющая (k = 0) (см. рис. 4.3)
Для второй гармоники (k = 2) комплексная амплитуда входного тока
где
Аналогично, для четвертой гармоники (k = 4)
Для шестой гармоники (k = 6)
Мгновенное значение входного тока для четырех гармоник дается выражением
После подстановки выражение примет вид
Вычислим для переменной составляющей приложенного напряжения коэффициенты формы, искажения, амплитуды.
Действующее значение входного напряжения
Для двухполупериодного выпрямления:
коэффициенты формы
коэффициенты амплитуды
коэффициенты искажения
Задача 4.3 Для линейной электрической цепи (рис. 4.4), подключенной к периодическому несинусоидальному напряжению, необходимо:1. Разложить входное напряжение u(t) в ряд Фурье.
2. Рассчитать мгновенные значения токов ветвей цепи.
3. Определить показания электродинамических амперметра и вольтметра.
4. Найти активную мощность, отдаваемую источником.
5. Вычислить для переменной составляющей приложенного напряжения коэффициенты формы, искажения, амплитуды.
6. Построить кривую выходного напряжения и определить его действующее значение.
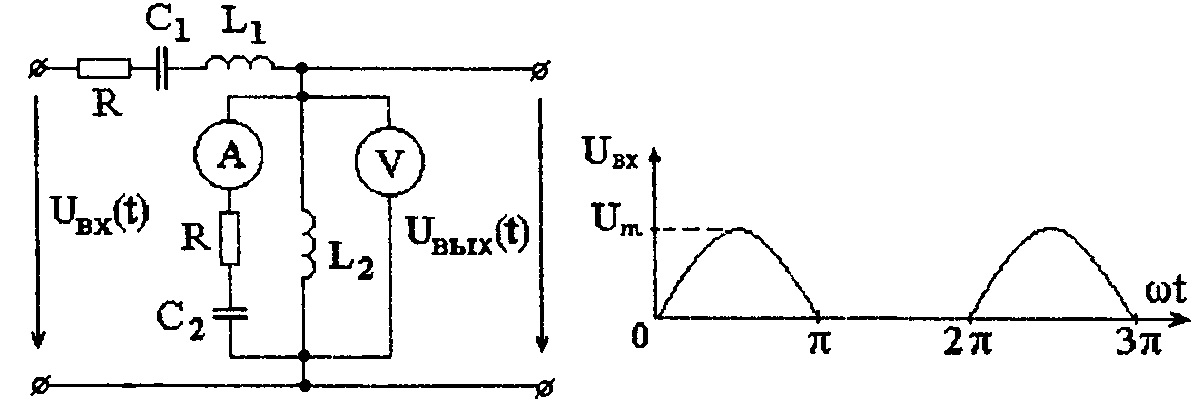
Рис. 4.4 Линейная электрическая цепь, подключенная к периодическому несинусоидальному напряжению
Дано:
f = 300 Гц; ω = 1884 с–1; L1 = 0,02 Гн; L2 = 0,002 Гн; R = 90 Ом; C1 = 10 мкФ = 10·10–6 Ф; C2 = 50 мкФ = 50·10–6 Ф; Um = 110 В,
Решение Разложим входное напряжение в ряд Фурье и запишем его первые четыре составляющие.
Для нахождения членов ряда Фурье воспользуемся формулами
где среднее значение функции за период или постоянная составляющая, называемая нулевой гармоникой,
амплитуды косинусоидальных и синусоидальных составляющих соответственно
амплитуда n-й гармоники спектра
начальная фаза n-й гармоники
угловая частота первой гармоники
здесь
f — циклическая частота первой гармоники спектра или основная частота,
T — период повторения функции f(t),
t0 — любой произвольно выбранный момент времени (обычно t0 = 0),
n = 1, 2, 3,… — номер гармоники.
Постоянная составляющая (нулевая гармоника)
Амплитуды синусоидальных составляющих напряжения
Амплитуды косинусоидальных составляющих напряжения
Получили разложение по первым пяти гармоникам входного напряжения
Комплексное входное сопротивление гармоникам тока
Комплексные амплитуды гармоник входного тока
Гармоники тока через катушку индуктивности по формуле разброса токов (делителя токов)
Гармоники тока через емкость по формуле разброса токов (делителя токов)
Мгновенные значения токов ветвей цепи
Комплексные амплитуды гармоник напряжений
Определим показания электродинамических амперметра и вольтметра
Найдем активную мощность, отдаваемую источником,
где сдвиг фаз между током и напряжением гармоник
Активная мощность нагрузки
где действующие значения токов
Численный расчет баланса мощностей
Pист = Pнагр = 18,7 Вт.
Вычислим для переменной составляющей приложенного напряжения коэффициенты формы, искажения, амплитуды.
Действующее значение входного напряжения
Для однополупериодного выпрямления:
коэффициенты формы
коэффициенты амплитуды
коэффициенты искажения
И, наконец, по полученному в ходе решения аналитическому выражению для выходного напряжения, построим график его изменения (рис. 4.5)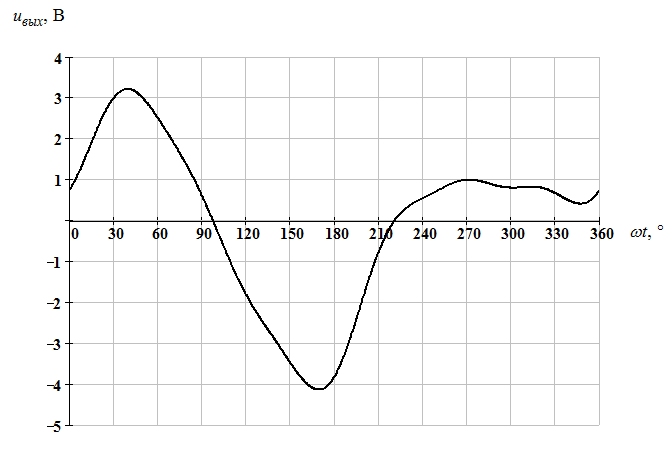
Рис. 4.5 График несинусоидального периодического выходного напряжения
Задача 4.4 К генератору с напряжением
подключена цепь, собранная по схеме рис. 4.6.
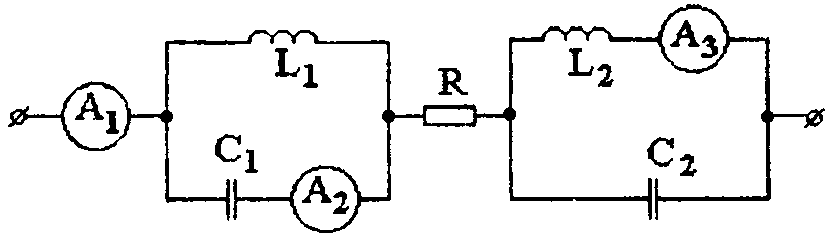
Рис. 4.6 Схема цепи, подключенной к генератору напряжения
Найти показания трех амперметров электродинамической системы.
Параметры элементов цепи: L1 = 40 мГн, C1 = 25 мкФ, R =30 Ом, L2 = 10 мГн, C2 = 6,25 мкФ.
Решение Расчет цепи производим, начиная с постоянной составляющей. Ток постоянной составляющей проходит через катушку L1, активное сопротивление R и катушку L2. Ограничен он только сопротивлением R. Следовательно, постоянная составляющая тока (ток нулевой гармоники)
Находим сопротивление элементов цепи первой гармонике
Дальнейшее определение сопротивлений элементов цепи первой гармонике не имеет смысла, так как оказалось, что первый контур настроен на частоту первой гармоники и поэтому его общее сопротивление первой гармонике равно бесконечности (резонанс токов) и напряжение первой гармоники приложено к первому контуру. Ток первой гармоники будет циркулировать только в первом контуре и не пойдет ни через амперметр А1, ни через амперметр А3.
Действующее значение тока первой гармоники через второй амперметр
Находим теперь сопротивления элементов цепи второй гармонике
Сопротивление всей цепи второй гармонике
чисто активное, то есть на частоте второй гармоники в цепи имеет место резонанс напряжений.
Неразветвленный ток второй гармоники в цепи
Падение напряжения на первом контуре
Ток второй гармоники через второй амперметр
Параметры цепи заданы такими, что ток второй гармоники через третий амперметр оказался равным той же величине
Сопротивление цепи четвертой гармонике равно бесконечности, так как второй контур настроен на частоту четвертой гармоники
Поэтому ток четвертой гармоники будет проходить только через третий амперметр второго контура
Найденные действующие значения токов отдельных гармоник через амперметры и показания этих амперметров, определенные по формуле
и выраженные в амперах, приведены в таблице 4.1.
Таблица 4.1 — Действующие значения токов отдельных гармоник через амперметры и показания этих амперметров
|
Ток через амперметр отдельных гармоник, А |
А1 |
А2 |
А3 |
|
I0 |
1 |
0 |
1 |
|
I(1) |
0 |
2,12 |
0 |
|
I(2) |
1,41 |
1,88 |
1,88 |
|
I(4) |
0 |
0 |
0,71 |
|
Показания амперметра |
1,73 |
2,83 |
2,25 |
Задача 4.5 Напряжение, приложенное к двум индуктивно связанным контурам (рис. 4.7), изменяется по закону
u = 100 + 70,7sinωt, В.
Параметры контуров: R1 = 40 Ом, R2 = 60 Ом, ωL1 = 30 Ом, ωL2 = 60 Ом, ωM = 20 Ом.
Найти выражения мгновенных токов в каждом из контуров.
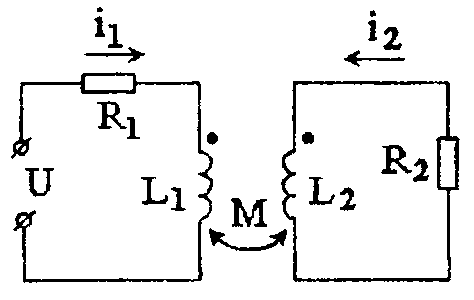
Рис. 4.7 Индуктивно связанные контуры
Решение Все токи по величине и фазе определяются для каждой гармоники в отдельности.
Постоянная составляющая тока, проходящая в первом контуре, во вторичном контуре ЭДС не наводит.
Уравнения для двух контуров (для основной гармоники) имеют вид
или
Решая эти уравнения, получим
Постоянная составляющая тока в первом контуре
Мгновенный ток в первом контуре
и, соответственно, во втором
Задача 4.6 Электрический мост, собранный из четырех одинаковых активных сопротивлений, питается двумя одинаковыми генераторами, включенными в диагонали мостика (рис. 4.8).
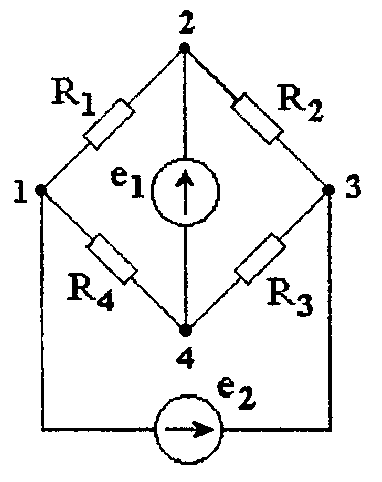
Рис. 4.8 Электрический мост из четырех активных сопротивлений питается двумя генераторами, включенными в диагонали мостика
ЭДС генераторов несинусоидальны. Если за положительные направления их принять направления, указанные стрелками на рис. 4.8, то окажется, что e2 отстает по фазе на T/2 от e1, а ЭДС e1 можно записать в форме ряда
Записать уравнения токов в сопротивлениях R1 и R2, и определить мощности, потребляемые ветвями моста, при Еm(1) = 100 В, Еm(2) = 10 В, R1 = R2 = R3 = R4 = 20 Ом.
Решение По условию задачи сопротивления в плечах моста равны друг другу, а, значит, мост уравновешен на любой частоте. Решаем задачу методом наложения. ЭДС второго генератора e2 отстает от e1 на T/2. Следовательно,
Далее, если при действии первого генератора за положительные направления токов в ветвях выбрать направления от узла 2 к узлу 1, от узла 2 к узлу 3, от узла 1 к узлу 4 и от узла 3 к узлу 4, то окажется, что при действии второго генератора положительными токами мы должны считать токи от узла 3 к узлу 2, от узла 3 к узлу 4, от узла 2 к узлу 1 и от узла 4 к узлу 1.
Таким образом, токи соответствующих гармоник в ветвях 2 — 1 и 3 — 4 будут алгебраически складываться, а в ветвях 1 — 4 и 2 — 3, соответственно, вычитаться. Очевидно, что при этом токи первого генератора через сопротивления R1 и R2 численно равны
а токи второго
А, значит, при работе двух генераторов уравнение тока через сопротивление R1 будет иметь вид
i1 = 0,5sin2ωt,
а уравнение тока через сопротивление R2
i2 = 5sinωt.
Мощности
P1 = P3 = 2,5 Вт, P2 = P4 = 250 Вт.
Задача 4.7 Определить показания амперметра электродинамической системы, включенного с помощью измерительного трансформатора в цепь, содержащую идеальный вентиль и активное сопротивление (рис. 4.9).
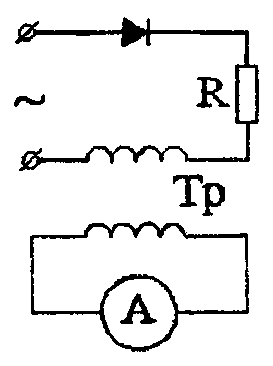
Рис. 4.9 Амперметр электродинамической системы, включенный с помощью измерительного трансформатора в цепь, содержащую идеальный вентиль и активное сопротивление
К цепи приложено синусоидальное напряжение амплитудой Um = 660 В. Активное сопротивление цепи R = 100 Ом Коэффициент трансформации трансформатора n = 1. Коэффициент связи между его обмотками можно считать равным 100%. Активным сопротивлением обмоток трансформатора и сопротивлением амперметра можно пренебречь.
Решение Ток в первичном контуре ограничен только активным сопротивлением, так как сопротивление трансформатора со вторичной короткозамкнутой обмоткой с коэффициентом связи, равным k = 1, равно нулю (см. входное сопротивление связанных контуров).
Ток во вторичном контуре будет отличаться от тока в первичном только отсутствием постоянной составляющей. Действующее значение тока в первичной обмотке в случае однополупериодного выпрямления
В то же время
где
Действующее значение тока во вторичной цепи
что и покажет амперметр.
 коэффициент амплитуды,
коэффициент формы,
Примеры расчета схем при несинусоидальных периодических воздействиях,
расчет цепи с несинусоидальными периодическими источниками,
расчет цепей несинусоидального тока,
несинусоидальный периодический ток,
постоянная составляющая тока,
расчет гармоник тока,
коэффициент искажения,
гармоники тока,
гармоники напряжения
коэффициент амплитуды,
коэффициент формы,
Примеры расчета схем при несинусоидальных периодических воздействиях,
расчет цепи с несинусоидальными периодическими источниками,
расчет цепей несинусоидального тока,
несинусоидальный периодический ток,
постоянная составляющая тока,
расчет гармоник тока,
коэффициент искажения,
гармоники тока,
гармоники напряжения
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
