3.3 Резонанс в электрической цепи
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 3 Методы расчета линейных цепей синусоидального тока3.3 Резонанс в электрической цепи
При резонансе характер нагрузки становится чисто активным, напряжение на входе цепи совпадает с током цепи
Решение задач резонанса в электрической цепи
Задача 3.3.1 Для последовательного колебательного контура (рис. 3.3.1) найти наибольшее напряжение на конденсаторе при изменении его емкости.
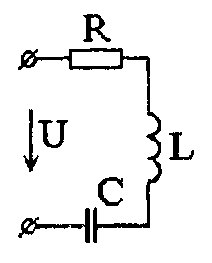
Рис. 3.3.1 Последовательный колебательный контур
Рассчитать и построить зависимость напряжения на конденсаторе от его емкости, если U =16 В, R = 50 Ом, L = 10 мГ, ω = 104 с–1.
Решение. Ток в последовательном контуре
Напряжение на емкости
(1)
Максимум напряжения на емкости найдем из условия
откуда
видно, что напряжение на конденсаторе достигает максимума при
Тогда
Кривая UC(ХC), рассчитанная по формуле (1), приведена на рис. 3.3.2.
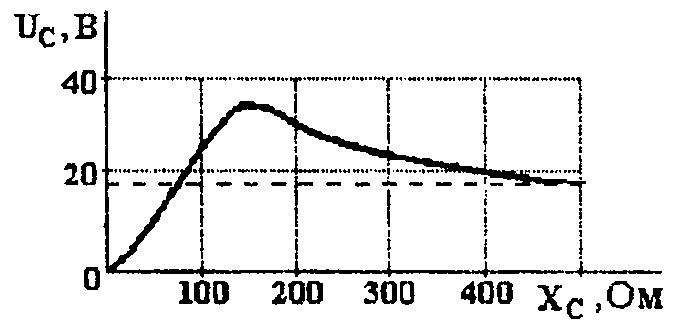
Рис. 3.3.2 Зависимость напряжения на конденсаторе от его емкости в последовательном колебательном контуре
Задача 3.3.2 В последовательной резонансной цепи (рис. 3.3.1) R = 2 Ом, C = 100 мкФ, L = 40 мГн.
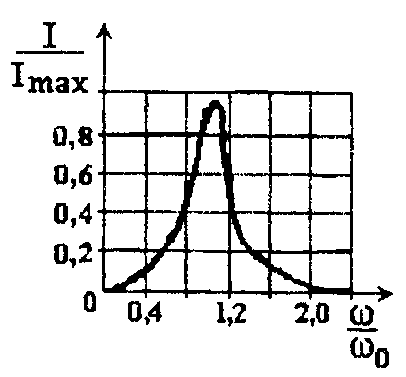
Определить резонансную частоту ω0 добротность контура, полосу пропускания и зависимость полосы пропускания от добротности контура. Построить резонансную кривую I/Imax = f(ω/ω0) при U =10 В. Построить векторные диаграммы напряжений при частотах ω0/2, ω0, 2 ω0.
Решение. Резонансная частота контура
Добротность контура
Резонансная кривая может быть построена из уравнения
Преобразуем это выражение
в относительных единицах Ω = ω/ω0
(2)
где ток при резонансе
Задаваясь разными значениями ω/ω0, находим I/Imax. Результаты расчетов сведены в табл. 1.
Таблица 1
|
Ω = ω/ω0 |
0,4 |
0,8 |
1,0 |
1,2 |
1,6 |
2,0 |
|
I/Imax |
0,047 |
0,217 |
1,0 |
0,263 |
0,102 |
0,066 |
По определению полосы пропускания из уравнения (2) имеем
или
Отсюда
или (3)
где ω1 и ω2 — граничные частоты полосы пропускания;
(4)
Решая совместно уравнения (3) и (4), найдем
Векторные диаграммы построены на рис. 3.3.3.
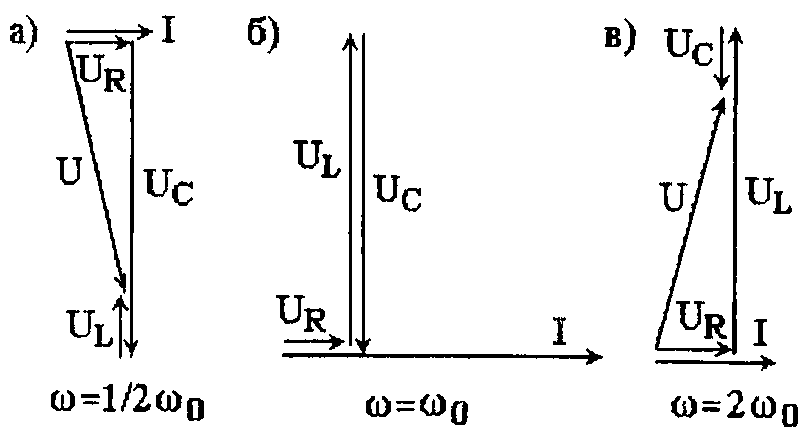
Рис. 3.3.3 Векторные диаграммы последовательного колебательного контура
Кривая I/Imax = f(ω/ω0) — на рис. 3.3.4.
 Резонанс в электрической цепи,
последовательный колебательный контур
Резонанс в электрической цепи,
последовательный колебательный контур
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
