3.2 Символический метод расчета цепей синусоидального тока
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 3 Методы расчета линейных цепей синусоидального тока3.2 Символический метод расчета цепей синусоидального тока
При расчете линейных цепей символическим методом токи, напряжения, ЭДС и сопротивления входят в уравнения электрического состояния в виде комплексов. Основными законами, применяемыми для расчета электрических цепей, являются законы Ома и Кирхгофа
Решение задач символическим методом
Задача 3.2.1 Для схемы рис. 3.2.1 определить токи во всех ветвях и напряжения на всех участках, составить баланс активных и реактивных мощностей, построить векторную диаграмму цепи на комплексной плоскости, записать мгновенные значения токов, если u = Umsin(ωt + ψU), Um =600 В, ψU = –90°, R1 = 10 Ом, Х2 = R3 = Х3 = 20 Ом, Х4 = 50 Ом.
Задачу решить символическим методом.
Примечание. Решение этой задачи методом векторных диаграмм приведено в 3.1 Расчет цепей синусоидального тока методом векторных диаграмм
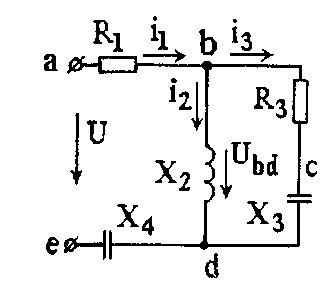
Рис. 3.2.1 Схема электрической цепи
Решение
Задачу решаем символическим методом в комплексных амплитудах.
Мгновенное значение напряжения
тогда комплексная амплитуда напряжения
Комплексные сопротивления ветвей
Эквивалентная электрическая схема представлена на рис. 3.2.2.
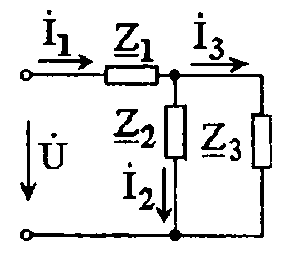
Рис. 3.2.2 Эквивалентная электрическая схема
Для схемы со смешанным соединением комплексное общее сопротивление
Комплексная амплитуда общего тока по закону Ома
Комплексные амплитуды токов ветвей по формуле делителя токов
Проверка по первому закону Кирхгофа
Действующие значения токов в ветвях
По формуле перехода от комплексных амплитуд к мгновенным значениям
мгновенные значения токов
Комплексная полная мощность источника
откуда активная мощность источника
реактивная мощность источника
Активная мощность потребителей
Реактивная мощность потребителей
Для построения топографической диаграммы на комплексной плоскости необходимо рассчитать комплексные действующие значения потенциалов точек схемы
При построении векторной диаграммы на комплексной плоскости учитываем направления векторов напряжения на пассивных элементах. Например, вектор напряжения на комплексной плоскости направлен от точки b к точке a, а вектор напряжения на комплексной плоскости направлен от точки d к точке b.
Топографическая диаграмма на комплексной плоскости приведена на рис. 3.2.3.
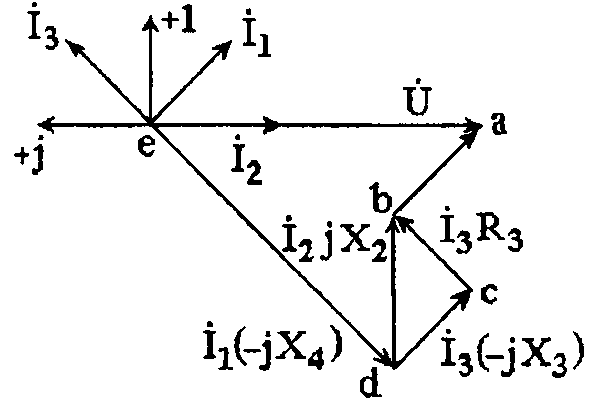
Рис. 3.2.3 Топографическая диаграмма на комплексной плоскости
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля

