1.6 Методы расчета нелинейных электрических цепей постоянного тока
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях1.6 Методы расчета нелинейных электрических цепей постоянного тока
Простые нелинейные электрические цепи постоянного тока рассчитывают графическим способом. При этом считаются известными вольт-амперные характеристики (ВАХ) нелинейных элементов, входящих в нелинейную цепь постоянного тока.
Нелинейный элемент, ВАХ которого в рабочем диапазоне приближенно можно изобразить прямолинейным участком, заменяют последовательным соединением линейного резистивного элемента с источником ЭДС. При этом сопротивление линейного элемента принимается равным дифференциальному сопротивлению нелинейного элемента в рабочей точке его ВАХ.
Нелинейный элемент в области рабочей точки характеристики можно также заменить параллельным соединением источника тока с линейным элементом, проводимость которого равна дифференциальной проводимости нелинейного элемента в этой точке.
Разветвленная нелинейная электрическая цепь постоянного тока с одним нелинейным элементом может быть рассчитана методом эквивалентного генератора. При этом заменяют линейную часть нелинейной цепи постоянного тока по отношению к нелинейному элементу эквивалентным источником. Полученную цепь последовательного соединения источника, линейного и нелинейного элементов рассчитывают графически.
Решение нелинейных уравнений, описывающих нелинейную электрическую цепь постоянного тока с двумя узлами, также проводят графически. При этом все уравнения необходимо строить в одинаковом масштабе, на одном графике в функции узлового напряжения.
Расчет нелинейных цепей постоянного тока
Задача 1.6.1 Графический метод расчета (для двух узлов) нелинейной цепи постоянного тока
Определить графическим методом значение токов в нелинейной цепи постоянного тока, показанной на рис. 1.6.1, если E1 = E3 = 100 В и R3 = 500 Ом.
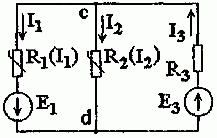
Рис. 1.6.1
Вольт-амперные характеристики нелинейных элементов симметричны относительно начала координат и показаны на рис. 1.6.2 (I1 (U1) — кривая 1; I2 (U2) — кривая 2).
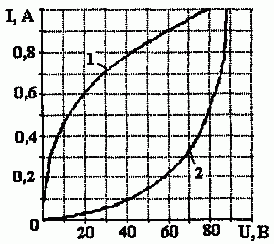
Рис. 1.6.2
Решение. Для всех трех ветвей цепи напряжение Ucd одинаково (см. рис. 1.6.1).
Построим вольт-амперные характеристики ветвей I1 (Ucd); I2 (Ucd); I3 (Ucd) (рис. 1.6.3).
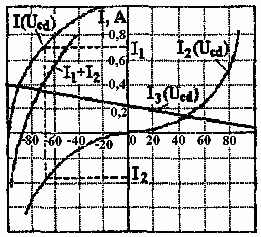
Рис. 1.6.3
Характеристика второй ветви I2 (Ucd) построена для нелинейного элемента 2.
Для первой ветви Ucd = U1 — E1. Из соответствующих значений U1 вольт-амперной характеристики 1 вычитаем E1. Результаты расчета характеристики I1 (Ucd) приведены в табл. 1.6.1.
Таблица 1.6.1
|
U1, В |
100 |
80 |
60 |
40 |
30 |
20 |
10 |
5 |
0 |
|
Ucd = U1 — E1 |
0 |
-20 |
-40 |
-60 |
-70 |
-80 |
-90 |
-95 |
-100 |
|
I1, А |
1,1 |
1,0 |
0,9 |
0,8 |
0,72 |
0,6 |
0,45 |
0,3 |
0 |
Продолжение табл. 1.6.1
|
U1, В |
-5 |
-10 |
-20 |
-30 |
-40 |
-60 |
-80 |
-100 |
|
Ucd = U1 — E1 |
-105 |
-110 |
-120 |
-130 |
-140 |
-160 |
-180 |
-200 |
|
I1, А |
-0,3 |
-0,4 |
-0,6 |
-0,72 |
-0,8 |
-0,9 |
-1,0 |
-1,1 |
По данным таблицы строим вольт-амперную характеристику первой ветви I1 (Ucd).
Третья ветвь является линейной, ее вольт-амперная характеристика Ucd (I3) = E3 — R3·I3. Для построения ВАХ по точкам пересечения прямой и осей координат находим
По первому закону Кирхгофа I1 + I2 = I3 построим зависимость I1 + I2 = f (Ucd), т. е. эквивалентную вольт-амперную характеристику первых двух ветвей. Эту характеристику получаем, складывая ординаты характеристик I1 (Ucd) и I2 (Ucd). В точке пересечения зависимостей I1 + I2 = f (Ucd) и I3 (Ucd) выполняется равенство I1 + I2 = I3, т. е. точка пересечения дает значения токов. Таким образом,
Ucd = –72 В; I1 = 0,68 А; I2 = –0,32 А; I3 = 0,36 А.
Задача 1.6.2 Приведение нелинейной цепи постоянного тока к графическому методу расчета для двух узлов
Определить значения токов во всех ветвях нелинейной цепи постоянного тока рис. 1.6.4.
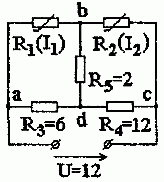
Рис. 1.6.4
Величины сопротивлений и входного напряжения указаны на рис. 1.6.4.
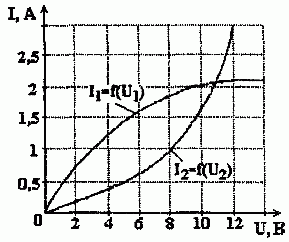
Рис. 1.6.5
Вольт-амперные характеристики нелинейных элементов показаны на рис. 1.6.5 в виде кривых I1 = f (U1); I2 = f (U2).
Решение. Для определения токов I1 и I2 в ветвях с нелинейными элементами разомкнем эти ветви и найдем напряжения U1х и U2х из схемы рис. 1.6.6
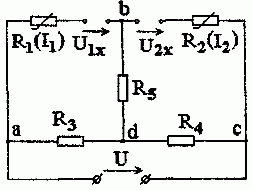
Рис. 1.6.6
2. Включим в соответствующие ветви с нелинейными элементами ЭДС E1х = U1х и E2х = U2х и замкнем накоротко зажимы a и c, к которым присоединен внешний источник напряжения (рис. 1.6.7).
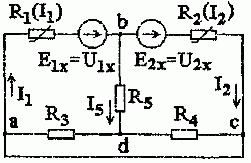
Рис. 1.6.7
Токи I1 и I2 в этой схеме будут равны действительным токам в соответствующих ветвях заданной схемы. После замены двух параллельных ветвей с сопротивлением R3 и одной эквивалентной ветвью получаем схему с двумя узлами (рис. 1.6.8), где
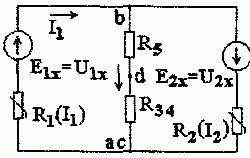
Рис. 1.6.8
Пользуясь схемой рис. 1.6.8, можно токи I1 и I2 определить графически, как это было сделано в предыдущей задаче 1.6.1.
Задача 1.6.3 Расчет нелинейной цепи постоянного тока методом линеаризации
Рассчитать ток I и напряжения U1 и U2 в цепи рис. 1.6.9, а, применив метод линеаризации. Характеристика нелинейного элемента показана на рис. 1.6.9, б.
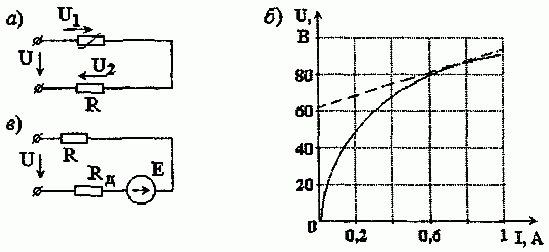
Рис. 1.6.9
Решение
1. Выбираем рабочую точку A (U = 86 В; I = 0,7 А) в почти линейной части вольт-амперной характеристики. Проводим в этой точке касательную, которая на оси ординат отсекает точку с напряжением U = 70 В. Для рабочей точки дифференциальное сопротивление
2. Исходную схему замещаем эквивалентной линейной (рис. 1.6.9, в). Для этой цепи
Напряжения на элементах
Полученная рабочая точка A лежит в линейной части вольт-амперной характеристики. Если полученные значения токов и напряжений не находятся в «окрестностях» рабочей точки, расчет необходимо повторить, выбрав другую рабочую точку.
Задача 1.6.4 Расчет нелинейной цепи постоянного тока методом итераций
Определить значение токов в нелинейной цепи постоянного тока методом итераций (рис. 1.6.10), если Е1 = 135 В; E2 =115 В.
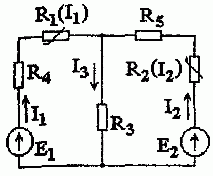
Рис. 1.6.10
Вольт-амперные характеристики нелинейных элементов даны на рис. 1.6.2: I1 (U1) — кривая 1; I2 (U2) — кривая 2.
Решение
1. Составим уравнения для данной цепи, применив законы Кирхгофа
Исключив переменную I3, число уравнений сокращаем до числа нелинейных элементов
2. Для обеспечения сходимости из первого уравнения находим U1, а из второго — I2
Текущие значения токов и напряжений обозначаем индексом k, а уточненные значения — индексом (k +1). Окончательно получаем
Значения I1k и U2k определяем из вольт-амперных характеристик соответствующих нелинейных элементов по известным U1k и I2k.
Сначала (k = 0) произвольно выбираем U10 = 40 В; I20 = 0,5 А.
Подставив их в итерационные уравнения, получаем
U11 = 50,2 В; I21 = 0,383 А.
Процедуру повторяем с уточненными значениями U12, I22 и т. д.
После семи шагов значения U1 и I2 будут изменяться незначительно. Вычисления прекращаем.
Таблица 1.6.2
|
k |
U1k, В |
I2k, А |
Из характеристик |
Из уравнения |
||
|
U2k, В |
I1k, А |
I2 (k+1), А |
U1 (k+1), В |
|||
|
0 |
40 |
0,5 |
80 |
0,8 |
0,383 |
50,2 |
|
1 |
50,2 |
0,383 |
75 |
0,85 |
0,33 |
55,72 |
|
2 |
55,72 |
0,33 |
72 |
0,88 |
0,313 |
58,3 |
|
3 |
58,3 |
0,313 |
71 |
0,89 |
0,305 |
59,4 |
|
4 |
59,4 |
0,305 |
70,5 |
0,897 |
0,301 |
59,9 |
|
5 |
59,9 |
0,301 |
70,1 |
0,9 |
0,3 |
59,96 |
|
6 |
59,96 |
0,3 |
70,0 |
0,9 |
0,3 |
60,0 |
|
7 |
60,0 |
0,3 |
70,0 |
0,9 |
0,3 |
60,0 |
Результаты расчета нелинейной цепи постоянного тока методом итераций показаны в табл. 1.6.2. Из нее следует: U1 = 60 В; I2 = 0,3 А; из вольт-амперных характеристик (–I1) = 0,9 А; U2 = 70 В, а из первого уравнения законов Кирхгофа находим ток I3 = I1 + I2 = 1,2 А.
Ссылка на статью по нелинейным электрическим цепям постоянного тока НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля

