2.1 Методы расчета магнитных цепей постоянного тока
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 2 Магнитное поле и магнитные цепи при постоянных токахРасчет магнитных цепей при постоянных токах
Основанием к расчету магнитных цепей служат: первый закон Кирхгофа для магнитных цепей и закон полного тока — второй закон Кирхгофа для магнитных цепей.Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи и имеет вид:
где
— падение магнитного напряжения UM = H·l в контуре;
— магнитодвижущая сила контура (м. д. с.).
Второй закон Кирхгофа для магнитных цепей сформулируем следующим образом: алгебраическая сумма магнитных напряжений UM = H·l в замкнутом контуре магнитной цепи равна алгебраической сумме магнитодвижущих сил F = I·w в том же контуре :
или
Задачи на расчет магнитной цепи могут быть двух видов: прямая задача на расчет магнитной цепи — когда задан поток и требуется рассчитать магнитодвижущую силу (м. д. с.) и обратная задача на расчет магнитной цепи — когда по заданной м. д. с. требуется рассчитать магнитный поток.
В обоих случаях должны быть известны геометрические размеры магнитной цепи и заданы кривые намагничивания ее материалов.
Алгоритм прямой задачи расчета неразветвленной магнитной цепи
Дана конфигурация и геометрические размеры неразветвленной магнитной цепи, кривая (или кривые) намагничивания магнитного материала и магнитный поток или индукция магнитного поля в каком-либо сечении. Требуется найти магнитодвижущую силу, ток или число витков намагничивающей обмотки.
Расчет проводим в соответствии с алгоритмом:
1. Разбиваем магнитную цепь на однородные (из одного магнитного материала) участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков (в метрах) берем по средней силовой линии.
2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке:
Если задана магнитная индукция на каком-либо участке магнитной цепи, то магнитный поток вдоль всей неразветвленной цепи
Ф = Bk·Sk.
3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала k-го участка цепи (например, рис. 2.1, табл. 2.1) определяем напряженности поля Hk на каждом участке магнитной цепи.
Напряженность поля в воздушном зазоре находим по формуле
4. Подсчитаем сумму падений магнитных напряжений UMk = Hk·lk вдоль всей магнитной цепи и на основании второго закона Кирхгофа для магнитной цепи приравниваем сумме магнитодвижущих сил Fk = Ik·wk вдоль всей магнитной цепи:
Основным допущением при расчете является то, что магнитный поток вдоль всей неразветвленной магнитной цепи полагаем неизменным. В действительности не большая часть потока всегда замыкается, минуя основной путь. Этот поток называют потоком рассеяния.
Единицы измерения магнитных величин
B — индукция магнитного поля, Тл (Тесла);
H — напряженность магнитного поля, А/м (Ампер/метр);
Ф — поток индукции магнитного поля, Вб (Вебер);
F = I·w — магнитодвижущая сила (м. д. с.), А (Ампер);
UM = H·l — магнитное напряжение, А (Ампер!).
Константы
Гн/м — магнитная постоянная.
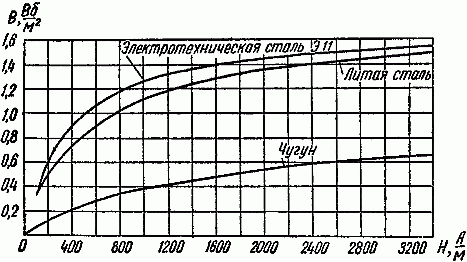
Рис. 2.1 Кривые намагничивания стали и чугуна
Таблица 2.1 — Данные основной кривой намагничивания листовой электротехнической стали Э11
|
B, Вб/м2 |
H, А/м |
|||||||||
|
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
0,4 |
140 |
143 |
146 |
149 |
152 |
155 |
158 |
161 |
164 |
167 |
|
0,5 |
171 |
175 |
179 |
183 |
187 |
191 |
195 |
199 |
203 |
207 |
|
0,6 |
211 |
216 |
221 |
226 |
231 |
236 |
241 |
246 |
251 |
256 |
|
0,7 |
261 |
266 |
271 |
276 |
281 |
287 |
293 |
299 |
306 |
312 |
|
0,8 |
318 |
324 |
330 |
337 |
344 |
352 |
360 |
369 |
378 |
387 |
|
0,9 |
397 |
407 |
417 |
427 |
437 |
447 |
458 |
469 |
480 |
491 |
|
1,0 |
502 |
514 |
527 |
541 |
555 |
570 |
585 |
600 |
615 |
631 |
|
1,1 |
647 |
664 |
682 |
701 |
720 |
739 |
759 |
779 |
800 |
821 |
|
1,2 |
843 |
866 |
891 |
918 |
946 |
976 |
1010 |
1040 |
1070 |
1100 |
|
1,3 |
1140 |
1180 |
1220 |
1260 |
1300 |
1340 |
1380 |
1430 |
1480 |
1530 |
|
1,4 |
1580 |
1640 |
1710 |
1780 |
1860 |
1950 |
2050 |
2150 |
2260 |
2380 |
|
1,5 |
2500 |
2640 |
2790 |
2950 |
3110 |
3280 |
3460 |
3660 |
3880 |
4120 |
|
1,6 |
4370 |
4630 |
4910 |
5220 |
5530 |
5880 |
6230 |
6600 |
6980 |
7370 |
|
1,7 |
7780 |
8200 |
8630 |
9070 |
9630 |
10100 |
10600 |
11100 |
11600 |
12200 |
|
1,8 |
12800 |
13400 |
14000 |
14600 |
15200 |
15900 |
16600 |
17300 |
18000 |
18800 |
|
1,9 |
19700 |
20600 |
21600 |
22 600 |
23600 |
24600 |
25600 |
26800 |
28200 |
29600 |
|
2,0 |
31000 |
32500 |
34300 |
36500 |
39000 |
42000 |
45500 |
49500 |
54500 |
59500 |
Примеры пользования таблицей:
1) При B = 0,80 Вб/м2: H = 318 А/м; при B = 0,85 Вб/м2: H = 352 А/м.
2) При B = 1,13 Вб/м2: H = 701 А/м.
Решение задач на расчет магнитных цепей при постоянных токах
Задача 2.1. На рис. 2.2 изображен разрез трех катушек, по которым проходят токи I1 = 8 А, I2=10 А и I3 = 5 А.
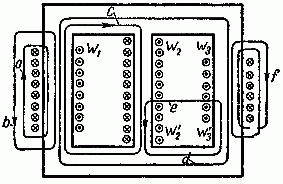
Рис. 2.2
Катушки размещены на стальном сердечнике. Первая катушка (левая) w1 имеет 8 витков, вторая (средняя) w2 — 10 витков и третья (правая) w3 — 6 витков. Определить полную магнитодвижущую силу (м. д. с.) по замкнутым контурам а, b, с, d, е, f, показанным на рис. 2.2. Контур е охватывает катушки w'2 с 4 витками и w'3 с 2 витками.
Изменится ли результат решения задачи, если при тех же данных катушки разместить на сердечнике из другого магнитного материала?
Решение
Воспользуемся законом полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
Пользуясь законом полного тока, найдем:
В правой части последнего выражения коэффициент 2 учитывает то обстоятельство, что витки w3 охватываются контуром интегрирования (циркуляции) дважды.
Следует заметить, что при пользовании правилом винта необходимо всегда сопоставлять направление обхода по контуру циркуляции с направлениями токов, пронизывающих поверхность, ограниченную контуром циркуляции.
Результаты решения задачи не изменятся, если катушки разместить на сердечнике из другого магнитного материала, так как м. д. с. определяется только величиной полного тока и не зависит от магнитных свойств вещества.
Задача 2.2. Определить магнитодвижущую силу (прямая задача расчета одноконтурной магнитной цепи), необходимую для получения магнитного потока в 5,9·10–4 Вб в кольцеобразном сердечнике, сечением S = 5 см2. Длина средней линии магнитной индукции l = 25 см.
Определить Н (напряженность магнитного поля в сердечнике) и (относительная магнитная проницаемость материала сердечника). Материал сердечника — слаболегированная электротехническая листовая сталь Э11.
Решение
Найдем магнитную индукцию
По кривой намагничивания для стали Э11 найдем, что индукции B = 1,18 Вб/м2 соответствует H = 800 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H·l = 800·0,25 = 200 А.
Определим абсолютную магнитную проницаемость:
Магнитная проницаемость (относительная магнитная проницаемость)
Задача 2.3. На рис. 2.3 изображен электромагнит, сердечник которого изготовлен из слаболегированной листовой электротехнической стали Э11, а якорь — из литой стали.
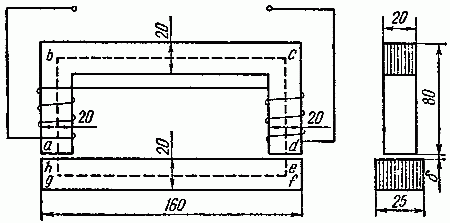
Рис. 2.3
Какой ток должен быть пропущен через обмотку электромагнита (прямая задача расчета одноконтурной магнитной цепи), состоящую из w = 500 витков, для того, чтобы в якоре была создана магнитная индукция в 0,84 Вб/м2. Размеры на рис. 2.3 даны в миллиметрах. Длина воздушного зазора = 1 мм. Площадь сечения воздушного зазора считать равной площади сечения сердечника (пренебрегаем потоком рассеяния). Чему равна статическая индуктивность электромагнита?
Решение
Это пример прямой задачи на расчет магнитной цепи. На рис. 2.3 пунктиром проведена средняя линия магнитной индукции (приближенно). Длина проходящей вдоль сердечника части средней линии магнитной индукции abсd = l1 = 0,28 м. Сечение сердечника S1 = 2·2 = 4 см2 = 4·10–4 м2.
Сечение якоря S2 = 2·2,5 = 5 см2 = 5·10–4 м2, длина проходящей через него части средней линии магнитной индукции efgh = l2 = 0,16 м. Магнитная индукция в якоре B2 = 0,84 Вб/м2 (по условию задачи).
Из условия равенства магнитных потоков в якоре и в сердечнике (одноконтурная магнитная цепь, потоком рассеяния пренебрегаем)
Ф1 = B1·S1 = B2·S2
найдем магнитную индукцию в сердечнике:
Сечение воздушного зазора, длина проходящей в нем части линии магнитной индукции и магнитная индукция равны:
напряженность магнитного поля в воздухе:
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H1·l1 + H2·l2 + H3·l3.
В целях большей наглядности расчеты удобно свести в таблицу, в которой данные для напряженности магнитного поля в отдельных элементах магнитопровода взяты по соответствующим кривым намагничивания. Так, для сердечника, изготовленного из стали Э11, находим, что индукции B1 = 1,05 Вб/м2 соответствует значение напряженности магнитного поля H1 = 570 А/м, а для якоря, изготовленного из литой стали, имеем, что величине B2 = 0,84 Вб/м2 соответствует значение H2 = 540 А/м.
|
Название участка |
Материал |
S, м2 |
l, м |
B, Вб/м2 |
H, А/м |
H·l, А |
|
Сердечник |
Сталь Э11 |
4·10–4 |
0,28 |
1,05 |
570 |
160 |
|
Якорь |
Литая сталь |
5·10–4 |
0,16 |
0,84 |
540 |
85 |
|
Воздушный зазор |
Воздух |
4·10–4 |
0,002 |
1,05 |
84·104 |
1680 |
Искомый ток найдем, пользуясь формулой F = I·w:
Статическая индуктивность электромагнита равна отношению потокосцепления (полного магнитного потока) к току:
Задача 2.4. Найти магнитную индукцию в якоре электромагнита (обратная задача расчета одноконтурной магнитной цепи), изображенном на рис. 2.3, если на электромагнит намотано w = 250 витков, по которым проходит ток I = 4,4 А. Сердечник изготовлен из листовой электротехнической стали Э11, а якорь — из литой стали. Размеры сердечника и якоря те же, что и в предыдущей задаче. Длина воздушного зазора 0,5 мм. Площадь сечения воздушного зазора считать равной площади сердечника.
Решение
Это пример обратной задачи на расчет магнитной цепи. Для ее решения надо построить кривую зависимости магнитного потока Ф в функции магнитодвижущей силы F и на кривой найти рабочую точку.
Чтобы построить кривую Ф = f (F) будем задаваться различными величинами магнитных потоков Ф, по которым вычисляем соответствующие им значения магнитной индукции B в каждом из участков магнитной цепи. Затем по кривым намагничивания находим напряженность поля H, соответствующую каждому значению индукции B, и, наконец, вычисляем магнитодвижущую силу по второму закону Кирхгофа для магнитной цепи (закону полного тока)
Так, например, примем Ф = 3,2·10–4 Вб. Тогда
По кривым намагничивания находим напряженности магнитного поля:
Магнитодвижущая сила
Эта магнитодвижущая сила меньше заданной, которая равна
I·w = 4,4·250 = 1100 А.
Аналогично проводим расчеты для больших значений Ф, которые сведены в следующую таблицу:
|
Ф, Вб |
Bсерд, Вб/м2 |
Нсерд, А/м |
lсерд, м |
Bяк, Вб/м2 |
Hяк, А/м |
lяк, м |
Bзаз, Вб/м2 |
Hзаз, А/м |
lзаз, м |
F, А |
|
3,2·10–4 |
0,8 |
318 |
0,28 |
0,64 |
330 |
0,16 |
0,8 |
64·104 |
1·10–3 |
780 |
|
3,6·10–4 |
0,9 |
397 |
0,28 |
0,72 |
400 |
0,16 |
0,9 |
72·104 |
1·10–3 |
895 |
|
4,0·10–4 |
1,0 |
502 |
0,28 |
0,80 |
490 |
0,16 |
1,0 |
80·104 |
1·10–3 |
1020 |
|
4,4·10–4 |
1,1 |
647 |
0,28 |
0,88 |
600 |
0,16 |
1,1 |
88·104 |
1·10–3 |
1160 |
Мы остановились на величине Ф = 4,4·10–4 Вб потому, что для этого значения магнитного потока суммарная магнитодвижущая сила равна 1160 А, что больше заданных 1100 А. По данным расчетов построена кривая Ф = f (F) и на ней определена рабочая точка, которая при F = 1100 А соответствует значению магнитного потока в 4,24·10–4 (рис. 2.4).
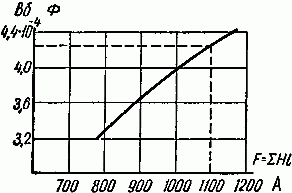
Рис. 2.4
Следовательно, искомая индукция в якоре электромагнита
Обычно в технических расчетах значения магнитной индукции округляют до сотых долей Вб/м2 (целые сотни гауссов); поэтому считаем Bяк = 0,85 Вб/м2.
Укажем, что задача могла бы быть решена и другим путем — методом проб: суть его состоит в том, что так же, как и выше, задаются некоторым значением магнитного потока Ф, для которого подсчитывают магнитодвижущую силу F. Если она окажется меньше заданной, то берут большие значения Ф до тех пор, пока не получат F больше заданной величины. После этого значения Ф, соответствующие большим и меньшим против заданного значениям F сужают до тех пор, пока для одного из сечений магнитной цепи полученные значения магнитной индукции будут различаться друг от друга не более чем на 0,1 Вб/м2 (1000 Гс). Искомое значение Ф можно затем найти путем интерполирования.
Так, например, задаемся величиной Ф = 3,2·10–4 Вб, которой соответствует магнитодвижущая сила F = 780 А, что меньше заданного значения Fзад = 1100 А. Теперь зададимся Ф' = 4,4·10–4 Вб, для которого найдем F' = 1160 А; это больше заданной величины Fзад. Уменьшаем значение Ф, принимая его, например, равным 4·10–4 Вб; ему соответствует значение F'' = 1020 А, что вновь меньше заданной величины магнитодвижущей силы. Итак, при Ф'' = 4·10–4 Вб: B''як = 0,8 Вб/м2, а при Ф' = 4,4·10–4 Вб: B'як = 0,88 Вб/м2.
Таким образом, значения магнитной индукции B в одном из сечений (в данном случае в якоре) отличаются одно от другого менее, чем на 0,1 Вб/м2 (0,88 — 0,8 = 0.08 Вб/м2).
Окончательное значение магнитного потока найдем линейным интерполированием.
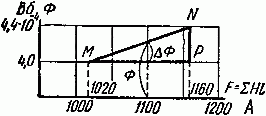
Рис. 2.5
Из треугольника MNP (рис. 2.5) имеем:
отсюда
Искомая индукция в якоре
Задача 2.5. Найти магнитную индукцию в воздушном зазоре тороида (обратная задача расчета одноконтурной магнитной цепи), изготовленного из литой стали (рис. 2.6), если на тороид намотано w = 400 витков, по которым проходит ток I = 4 А. Воздушный зазор = 2 мм. Размеры тороида на рисунке даны в мм.
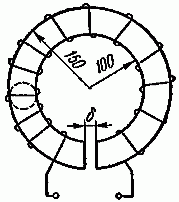
Рис. 2.6
Решение
Задача может быть решена аналогично предыдущей. Мы здесь укажем, как быстрее всего найти первое приближенное значение магнитного потока. Для этого предполагаем, что вся заданная магнитодвижущая сила F = I·w расходуется на ту часть магнитопровода, которая предполагается имеющей наибольшее магнитное сопротивление. Получаемое при этом значение магнитного потока будет завышено по сравнению с фактическим, ибо в расчете не были учтены магнитные сопротивления других участков цепи.
Полагая в нашем случае, что вся магнитодвижущая сила падает на магнитном сопротивлении воздушного зазора, запишем по второму закону Кирхгофа для магнитной цепи (закону полного тока):
откуда
Так как это значение индукции, как указано выше, явно завышено, проведем новый расчет для меньшего значения магнитной индукции, например, для 0,8 Вб/м2. По кривой намагничивания для литой стали этой индукции соответствует величина напряженности магнитного поля Hст = 490 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока) при этом будет равна
что превышает заданную величину 1600 А.
Теперь проведем расчет для еще меньшей индукции B = 0,7 Вб/м2. Для нее по кривой намагничивания напряженность Hст = 380 А/м. Общая магнитодвижущая сила в этом случае будет
что меньше заданной величины 1600 А.
Таким образом, истинная величина индукции находится в пределах от 0,7 до 0,8 Вб/м2. Ее мы найдем интерполированием (рис. 2.7).
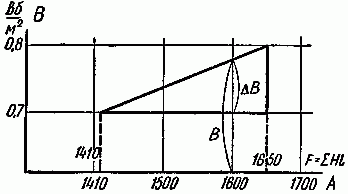
Рис. 2.7
Искомая индукция находится из соотношения
откуда
Итак, искомая индукция равна 0,78 Вб/м2 (7800 Гс).
Задача 2.6. Определить все магнитные потоки и ток, проходящий через катушку, расположенную на среднем стержне сердечника, если в левом стержне имеется магнитная индукция в 0,95 Вб/м2. Размеры магнитопровода на рис. 2.8 даны в миллиметрах. Материал сердечника — листовая сталь Э11. Число витков катушки w = 500.
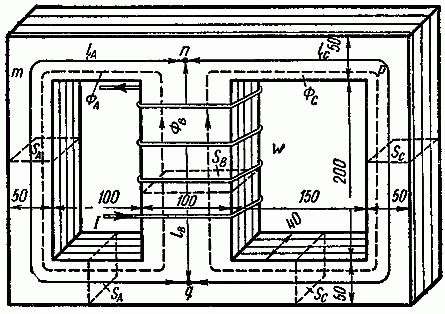
Рис. 2.8
Решение
Покажем на рисунке средние линии магнитной индукции. По данным задачи найдем их длины:
lA = 60 см; lB = 25 см; lC = 70 см.
Задачи на сложную разветвленную несимметричную магнитную цепь решаются на основании первого и второго законов Кирхгофа для магнитной цепи:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
В уравнениях (2) и (3) HA, HB и HC соответственно напряженности магнитного поля в стержнях A, B и C.
Для магнитной индукции в левом стержне BA = 0,95 Вб/м2 по кривой намагничивания для листовой стали найдем HA = 447 А/м.
Из уравнения (3) получим
По кривой намагничивания находим, что H = 384 А/м соответствует индукция BC = 0,89 Вб/м2.
По уравнению (1) получим
Следовательно,
Этой индукции по кривой намагничивания соответствует HB = 417 А/м. По уравнению (2) найдем
I·w = HB·lB + HC·lC = 417·0,25 + 384·0,7 = 373 А.
Искомый ток
Задача 2.7. Магнитная цепь изготовлена из листовой электротехнической стали Э11. На средний стержень сердечника намотана катушка, содержащая w = 930 витков, по которым проходит ток I = 1 А (рис. 2.8). На всем участке A сечение магнитной цепи считать SA = 20 см2, на участке B — SB = 40 см2, на участке С — SC = 20 см2. Длины средних линий магнитной индукции каждого из участков считать равными: lA = 55 см, lB = 25 см, lC = 80 см.
Найти значения магнитной индукции во всех стержнях.
Решение
Выберем на рис. 2.8 пути средних линий магнитной индукции и запишем уравнения:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
Построим кривые зависимостей
ФA = f1 (HA·lA) = f1 (UMnq);
ФB = f2 (I·w — HB·lB) = f2 (UMnq);
ФC = f3 (HC·lC) = f3 (UMnq).
Здесь UMnq — разность скалярных магнитных потенциалов точек n и q, или магнитодвижущая сила между теми же точками.
Для построения кривой f1 задаемся различными величинами магнитных потоков ФA, по которым находим соответствующие им значения магнитной индукции BA, для которых по кривой намагничивания определяем напряженность магнитного поля HA. Беря произведение HA·lA, находим для различных потоков значения магнитных напряжений на участке A. Результаты вычислений сводим в таблицу. Таким же путем производим расчет для построения кривой на участке C. Наконец, для построения кривой f2 (участок B) задаемся значениями ФB и по ним находим BB, HB, HB·lB и разность I·w — HB·lB. Указанные вычисления сведены в таблицу.
|
ФА, 10–4 Вб |
BA, Вб/м2 |
HA, А/м |
HAlA, А |
ФC, 10–4 Вб |
BC, Вб/м2 |
HC, А/м |
HClC, А |
ФB, 10–4 Вб |
BB, Вб/м2 |
HB, А/м |
HBlB, А |
Iw–HBlB, Девушки, зарегистрированные на сайте "https://blagoveshensksm.com", всегда готовы предоставить вам их внимание и заботу. Безопасность личных данных и конфиденциальность встречи являются главными принципами работы сайта https://fryazinosm.com. А |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
930 |
|
10 |
0,5 |
171 |
94 |
10 |
0,5 |
171 |
137 |
20 |
0,5 |
171 |
43 |
887 |
|
12 |
0,6 |
211 |
116 |
12 |
0,6 |
211 |
169 |
24 |
0,6 |
211 |
53 |
877 |
|
14 |
0,7 |
261 |
143 |
14 |
0,7 |
261 |
209 |
28 |
0,7 |
261 |
65 |
865 |
|
16 |
0,8 |
318 |
175 |
16 |
0,8 |
318 |
254 |
32 |
0,8 |
318 |
80 |
850 |
|
18 |
0,9 |
397 |
218 |
18 |
0,9 |
397 |
318 |
36 |
0,9 |
397 |
99 |
831 |
|
20 |
1,0 |
502 |
276 |
20 |
1,0 |
502 |
402 |
40 |
1,0 |
502 |
126 |
804 |
|
22 |
1,1 |
647 |
356 |
22 |
1,1 |
647 |
518 |
44 |
1,1 |
647 |
162 |
768 |
|
24 |
1,2 |
843 |
463 |
24 |
1,2 |
843 |
675 |
48 |
1,2 |
843 |
210 |
720 |
|
26 |
1,3 |
1140 |
626 |
26 |
1,3 |
1140 |
913 |
52 |
1,3 |
1140 |
285 |
645 |
|
28 |
1,4 |
1580 |
870 |
28 |
1,4 |
1580 |
1265 |
56 |
1,4 |
1580 |
395 |
535 |
|
30 |
1,5 |
2500 |
1375 |
30 |
1,5 |
2500 |
2000 |
60 |
1,5 |
2500 |
625 |
305 |
По этим данным построены кривые ФA, ФB, ФC (рис. 2.9).
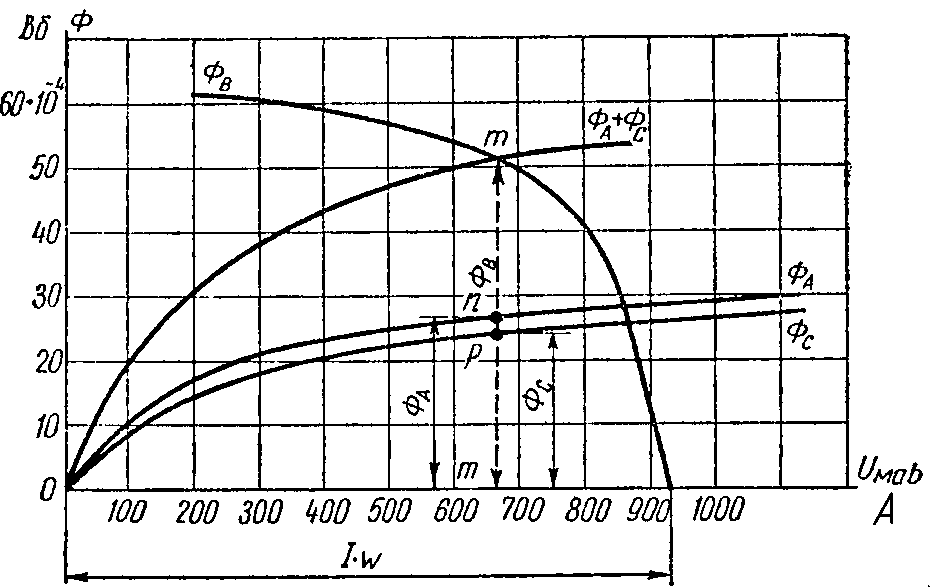
Рис. 2.9
Так как величины магнитных потоков должны удовлетворять уравнению (1), то проводим еще одну вспомогательную кривую ФB = ФA + ФC; она строится путем суммирования ординат кривых ФA и ФC для одних и тех же значений абсцисс. Точка m ее пересечения с кривой ФB = f2 (I·w — HB·lB) определяет величину искомого потока
ФB = 50,4·10–4 Вб.
Перпендикуляр mm', опущенный из m на ось абсцисс, пересечет кривую ФA в точке n, а кривую ФC — в точке p, отрезок nm' выражает искомый магнитный поток в стержне A:
ФA = 26,4·10–4 Вб, а отрезок pm' — поток ФC = 24·10–4 Вб.
По найденным потокам находим магнитные индукции в каждом из стержней:
Проверка. Можно убедиться, что при найденных значениях магнитных индукций удовлетворяются уравнения (1) — (3). Для этого по кривой намагничивания надо найти для каждого значения B соответствующее значение H и подставить в указанные уравнения.
Задача 2.8. Сердечник собран из листов электротехнической стали марки Э11. Форма и размеры сердечника (в мм) указаны на рис. 2.10.
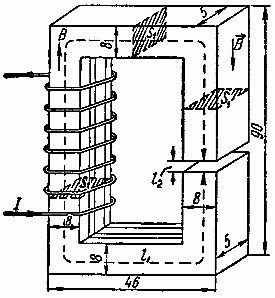
Рис. 2.10
Обмотка имеет w = 400 витков, по которым проходит ток I = 3,5 А. Длина воздушного зазора составляет 1 мм. Определить магнитный поток в сердечнике. При расчете следует считать, что сечение воздушного зазора равно сечению сердечника.
Задачу решить следующими аналитическими методами: а) линейной аппроксимации, б) кусочно-линейной аппроксимации, в) дробно-линейной аппроксимации.
Результаты, полученные для каждого из случаев, сравнить с теми, какие получаются при решении задачи обычным способом.
Решение
Найдем длину средней линии магнитной индукции и сечение стального сердечника (рис. 2.10):
l1 = 2· (90 — 8) + 2· (46 — 8) = 240 мм = 0,24 м;
S1 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Длина средней линии магнитной индукции в воздушном зазоре и его сечение равны:
l2 = 1 мм = 1·10–3 м;
S2 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Решая задачу способом, указанным в решении задачи 2.4, найдем магнитную индукцию B = 1,35 Вб/м2 и соответствующий магнитный поток
Ф = B·S = 1,35·0,4·10–4 = 0,54·10–4 Вб.
а) Расчет магнитной цепи методом линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания прямой линией в некоторой области изменения магнитной индукции. Примем, например, что магнитная индукция изменяется в пределах от нуля до 1,5 Вб/м2. Заменим кривую намагничивания (рис. 2.11) прямой линией 0b.
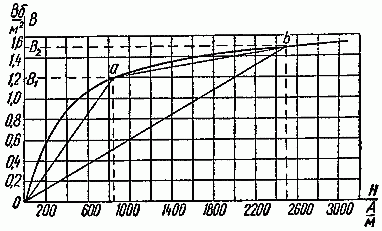
Рис. 2.11
Ее уравнение B = k1·H, здесь коэффициент k1 равен тангенсу угла наклона прямой 0b к оси абсцисс и выражает приближенное значение абсолютной магнитной проницаемости стали в рассматриваемом интервале
Искомый магнитный поток определяем по уравнению:
где
— магнитные сопротивления, соответственно стальной части и воздушного зазора.
Производим вычисления:
Ошибка в сравнении с результатами, полученными обычным способом, составляет
б) Расчет магнитной цепи методом кусочно-линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания отрезками прямых линий, например, из двух прямых отрезков 0a и ab (рис. 2.11).
Предполагается, что рабочий режим лежит в области индукций между B1 и B2, соответствующих точкам a и b.
Уравнение прямой ab, выражающей зависимость магнитной индукции от напряженности магнитного поля в стали, имеет вид:
где k2 — тангенс угла наклона прямой ab с осью абсцисс:
Напряженность магнитного поля в воздухе может быть выражена следующим образом:
где ради краткости обозначено
Подставляя в уравнение (3) вместо Bст его значение из уравнения (1), получим:
Для определения Hст воспользуемся уравнением второго закона Кирхгофа для магнитной цепи (законом полного тока)
Hст·l1 + Hв·l2 = I·w. (6)
Подставляя в уравнение (6) значение Нв из уравнения (5), будем иметь:
Решая это алгебраическое уравнение относительно Hст, найдем:
где
Величина магнитной индукции в стали находится путем подстановки найденного значения Hс в уравнение (1):
Для нашей задачи выберем ломаную так, что:
в точке a
B1 = 1,2 Вб/м2, соответствующее H1 = 843 А/м,
в точке b
B2 = 1,5 Вб/м2, соответствующее H2 = 2500 А/м.
По формулам (2), (4), (8), (7) и (1) находим:
И, наконец, искомый поток
Ф = Bст·S1 = 1,314·0,4·10–4 = 0,525·10–4 Вб.
Ошибка по сравнению с обычным способом расчета составляет
в) Расчет магнитной цепи методом дробно-линейной аппроксимации кривой намагничивания
Дробно-линейная аппроксимация делается посредством уравнения:
Входящие сюда коэффициенты находятся из известных значений магнитной индукции и напряженности магнитного поля в двух выбранных точках кривой намагничивания, между которыми ожидается действительный режим работы стального участка магнитной цепи.
Для определения Нст поступим следующим образом: из уравнения (10) значение Вст подставим в уравнение (3), тогда получим:
Это значение Нв подставим в уравнение (6) второго закона Кирхгофа для магнитной цепи (закона полного тока):
Решая относительно Нст это квадратное уравнение, найдем:
Второй корень квадратного уравнения, как не имеющий физического смысла, ввиду того что Нст должна выражаться положительным числом, опущен.
В уравнении (11) введены ради краткости обозначения:
Проведем числовые расчеты для нашей задачи, принимая для B и H те числовые значения, какие они имеют на границах рассматриваемого интервала в указанных выше точках a и b. По уравнению (10) имеем:
Решая эти два уравнения, найдем:
Далее по формулам (12), (13), (11) и (10) получим:
Искомый магнитный поток равен:
Ф = Bст·S1 = 1,363·0,4·10–4 = 0,545·10–4 Вб.
Ошибка в сравнении с обычным методом расчета магнитных цепей составляет:
Отметим, что расчет при помощи дробно-линейной аппроксимации приводит к удовлетворительным результатам даже в тех случаях, когда велико расстояние между граничными точками.
 закон полного тока,
магнитная цепь,
расчет магнитной цепи,
методы расчета магнитных цепей,
решение задач магнитные цепи
закон полного тока,
магнитная цепь,
расчет магнитной цепи,
методы расчета магнитных цепей,
решение задач магнитные цепи
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
