Главная → Теория электрических цепей → Единичная импульсная функция или дельта-функция

Единичная импульсная функция или дельта-функция

Единичная импульсная функция

Единичная импульсная функция, или дельта-функция δ(t) — это обобщенная функция единичной площади, равная ∞ при t = 0 и равная 0 при t ≠ 0.

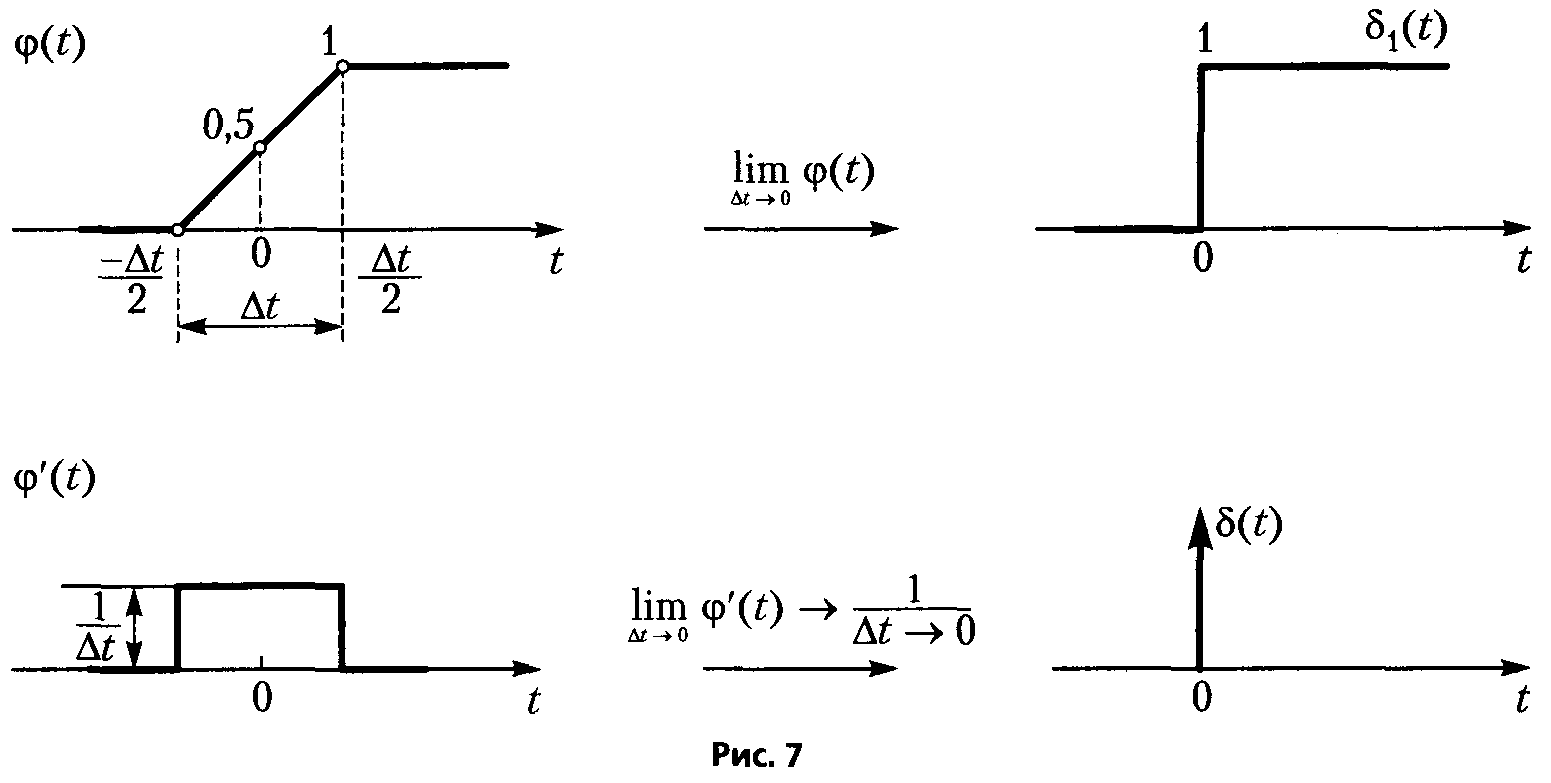
Получение единичной импульсной функции дифференцированием единичной ступенчатой функции

Вводится единичная импульсная функция (рис. 7) как предел последовательности производных φ'(t) от последовательности функций φ(t), при помощи которой была введена единичная ступенчатая функция δ₁(t) то есть единичная импульсная функция является производной от единичной ступенчатой функции

$\delta \left(t\right)=\frac{d{\delta }_1\left(t\right)}{dt}=\{\begin{array}{l}\mathrm{0,}t\ne 0;\\ \infty ,t=0.\end{array}$

Смещенная единичная импульсная функция

$\delta \left(t-t_0\right)=\frac{d{\delta }_1\left(t-t_0\right)}{dt}=\{\begin{array}{l}\mathrm{0,}t\ne t_0;\\ \infty ,t=t_0\end{array}$

имеет размерность [с^–1].

Применение единичной импульсной функции, опирающееся на свойства единичной импульсной функции, чрезвычайно многообразно, в частности, в теории дискретных цепей и дискретных сигналов (то есть в вычислительной технике), а также в импульсной технике и теории управления.

единичная импульсная функция, дельта-функция