Главная → Теория электрических цепей → Каскадное соединение четырехполюсников

Каскадное соединение четырехполюсников

Каскадное соединение четырехполюсников

Каскадное соединение четырехполюсников 1 и 2 (с матрицами параметров [a]₁ и [a]₂) изображено на рис. 18, а.

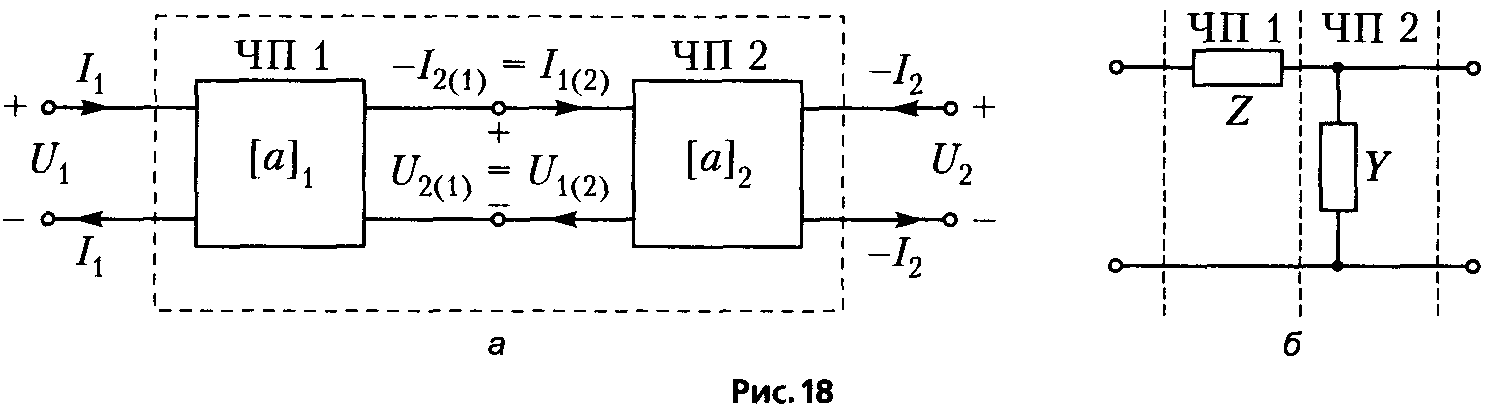
а) каскадное соединение четырехполюсников; б) четырехполюсник лестничной структуры как каскадное соединение простейших четырехполюсников

Это каскадное соединение всегда регулярно. При каскадном соединении выход четырехполюсника 1 является входом четырехполюсника 2 (у двухполюсников нет аналогичного соединения). Результирующая матрица a-параметров соединения [a] = [a]₁·[a]₂. При изменении последовательности каскадов будет иная результирующая матрица [a]₂·[a]₁ соединения (произведение матриц не является переместительным). Любой четырехполюсник лестничной структуры, например, изображенный на рис. 18, б, можно представить каскадным соединением простейших, тогда

$\left[a\right]={\left[a\right]}_Z\cdot {\left[a\right]}_Y=\left[\begin{array}{cc}1& Z\\ 0& 1\end{array}\right]\cdot \left[\begin{array}{cc}1& 0\\ Y& 1\end{array}\right]=\left[\begin{array}{cc}1+ZY& Z\\ Y& 1\end{array}\right].$

Каскадное соединение четырехполюсников