Главная → Примеры решения задач ТОЭ → НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Основные положения и соотношения

1. Кривая, выражающая функциональную зависимость напряжения от тока, называется вольт-амперной характеристикой элемента цепи.

Нелинейные элементы цепей могут иметь симметричные или несимметричные (относительно начала координат U = 0, I = 0) характеристики. Несимметричными характеристиками обладают так называемые полупроводниковые элементы цепей.

При расчете нелинейных цепей вводят следующие понятия:

а) Статическое сопротивление — отношение напряжения к току,

$r_{ст}\left(I\right)=\frac{U}{I}.$   (1)

б) Дифференциальное сопротивление (динамическое сопротивление) — предел отношения малого приращения напряжения к малому приращению тока при неограниченном уменьшении последнего,

$r_{д}\left(I\right)=\frac{dU}{dI}.$   (2)

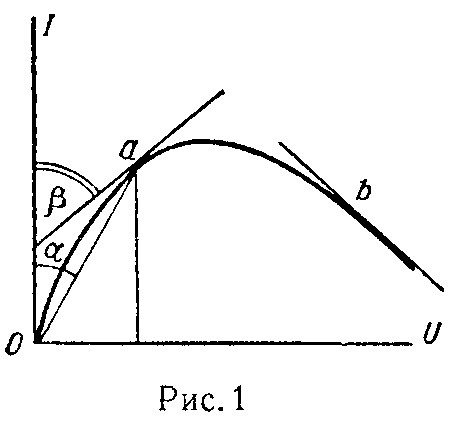
Для некоторой точки a характеристики (рис. 1) величина статического сопротивления пропорциональна тангенсу угла α, образованному лучом, проведенным из начала координат в данную точку, с осью токов

$r_{ст}\left(I\right)=k\cdot tg\alpha ,$   (3)

а величина динамического сопротивления пропорциональна тангенсу угла β, образованному касательной к характеристике в точке a с осью токов

$r_{д}\left(I\right)=k\cdot tg\beta ,$   (4)

где

$k=\frac{m_U}{m_I}.$   (5)

Здесь m_U — масштаб напряжений, m_I — масштаб токов.

Для пассивных элементов (т.е. не содержащих источников энергии) всегда r_ст > 0, a r_д > 0 — для точек, лежащих на восходящей части характеристики (рис. 1, точка a), r_д < 0 — для точек, лежащих па падающей части характеристики (рис. 1, точка b).

2. Графический метод расчета электрических цепей, состоящих из последовательно, параллельно или смешанно соединенных ветвей и участков, содержащих нелинейные элементы, производится следующим порядком: строятся характеристики отдельных элементов цепи, по которым, на основании соотношений, определяемых законами Кирхгофа, вычерчиваются характеристики цепи, состоящей из нескольких элементов, соединенных между собой тем или иным способом. Используя эти характеристики, можно определить величины напряжений и токов в отдельных участках цепи.

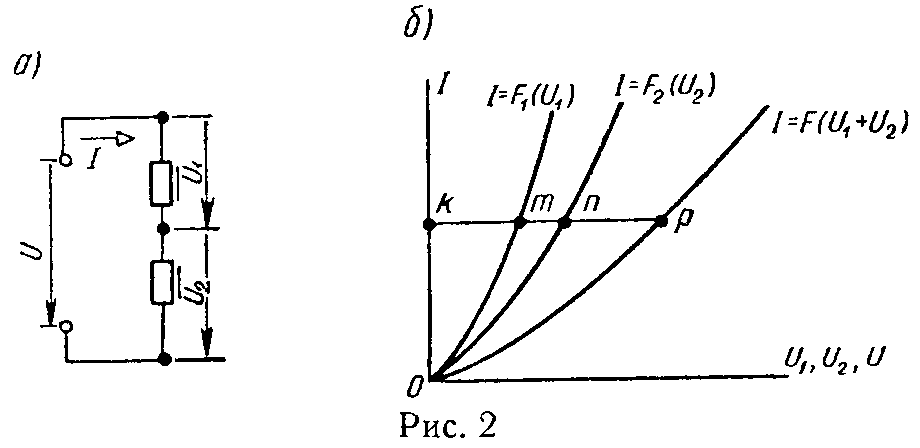
При последовательном соединении двух нелинейных элементов (рис. 2, а), характеристики которых I = F_l (U₁) и I = F₂ (U₂), строится характеристика I = F (U₁ + U₂), точки которой получатся путем сложения для каждого значения тока соответствующих им значений напряжений U₁ и U₂ (на рис. 2, б для любой точки характеристики km + kn = kp).

Пример — в задаче 4.

В случае последовательного соединения нелинейного элемента, характеристика которого I = F_l (U₁), с линейным сопротивлением r, включенными на напряжение U (рис. 3, а), помимо указанного, часто используется и другой путь.

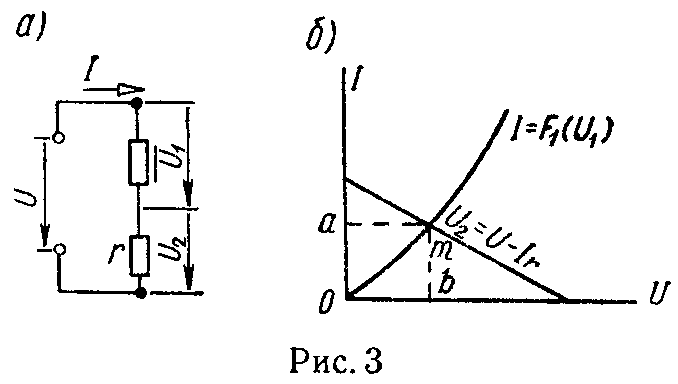
Строятся характеристика нелинейного элемента и прямая по уравнению U₂ = U — I·r (рис. 3, б). Точка их пересечения m определяет режим работы схемы (на рис. 3, б отрезок 0a в масштабе токов выражает ток, а отрезок 0b в масштабе напряжений — напряжение U₁ на нелинейном элементе).

Пример — в задаче 4.

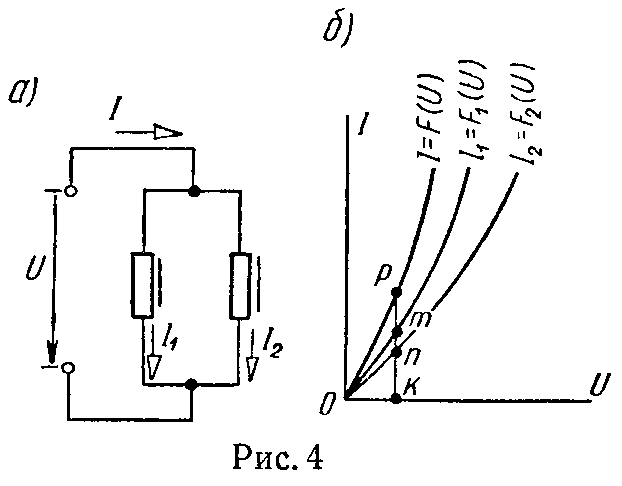
При параллельном соединении двух нелинейных элементов (рис. 4, а) по заданным характеристикам I₁ = F_l (U) и I₂ = F₂ (U) строится характеристика I = I₁ + I₂ = F (U) (рис. 4, б). Она получается из заданных путем сложения для каждого значения напряжения соответствующих им токов в параллельных ветвях (на рис. 4, б для любой точки характеристики km + kn = kp).

Пример — в задаче 6.

При смешанном соединении нелинейных элементов сначала строится характеристика для параллельных ветвей и затем — характеристика для последовательных элементов: заданного и эквивалентного параллельным ветвям.

Пример — в задаче 10.

3. В ряде практических задач в целях упрощения расчета цепи, содержащей нелинейные элементы, ее заменяют эквивалентной линейной цепью. Такая замена называется линеаризацией. В простейшем случае можно нелинейную вольт-амперную характеристику заменить ломаной линией, состоящей из ряда прямолинейных участков (кусочно-линейная аппроксимация); тогда в пределах каждого участка зависимость между током и напряжением выражается линейным уравнением.

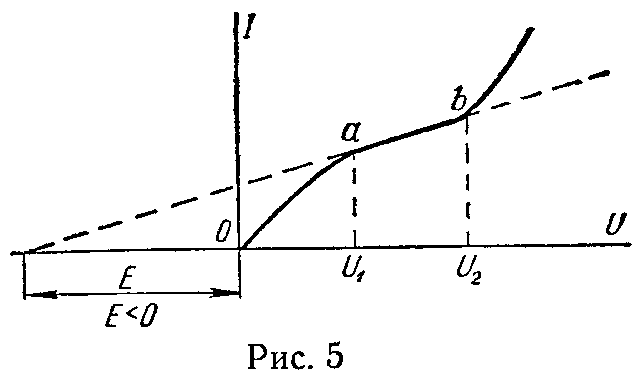
Так, в случае линеаризации участка ab характеристики в пределах U₁ < U < U₂ (рис. 5) уравнение прямой будет иметь следующий вид

$U=I\frac{dU}{dI}-E=I\cdot r_{д}-E,$   (6)

где производная $\frac{dU}{dI}=r_{д}$  – динамическое сопротивление, которое в пределах рассматриваемого интервала предполагается постоянным.

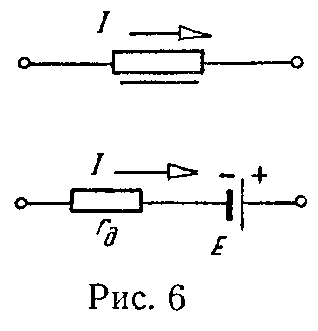
Нелинейный участок ab характеристики может быть заменен эквивалентной схемой, состоящей из линейного сопротивления r_д и э.д.с. E, включенным согласно схеме рис. 6.

Следует помнить, что замена справедлива лишь в таком режиме работы, когда напряжение на нелинейном элементе цепи лежит в пределах линеаризированного участка (U₁ < U < U₂, рис. 5). При выходе за эти пределы эквивалентная схема потеряет силу.

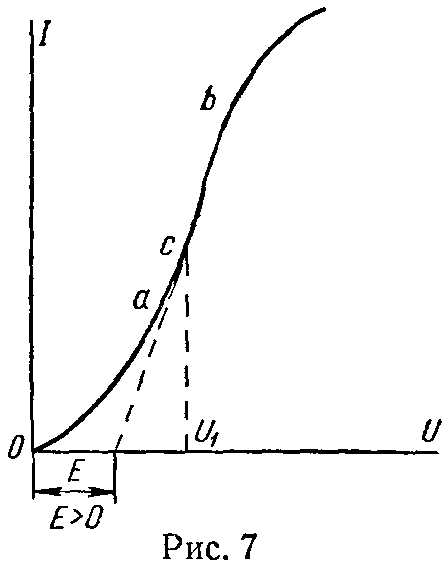
При линеаризации участка ab характеристики (рис. 7) вблизи точки c (соответствующей напряжению U₁) уравнение будет

$U=I\frac{dU}{dI}+E=I\cdot r_{д}+E,$   (7)

а нелинейный элемент цепи в этом режиме работы может быть заменен эквивалентной схемой по рис. 8.

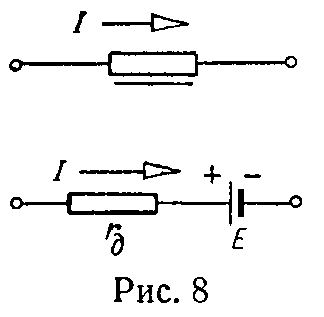
Пример — в задаче 16.

4. При последовательном соединении нелинейного элемента, характеристика которого задана, и источника с постоянной э.д.с. E (рис. 9), характеристика всей ветви строится на основании уравнения второго закона Кирхгофа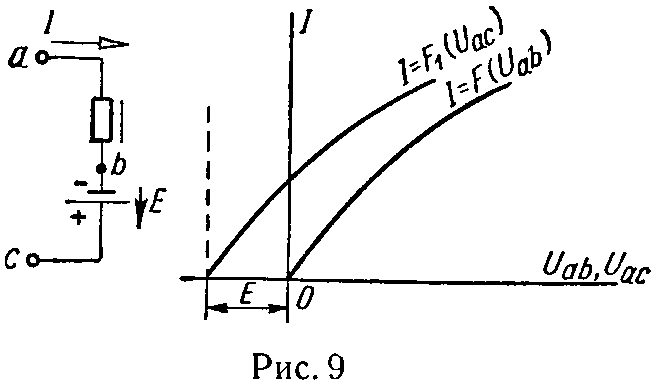

U_ac = U_ab — E.  (8)

Для рис. 10 характеристика ветви строится по следующему уравнению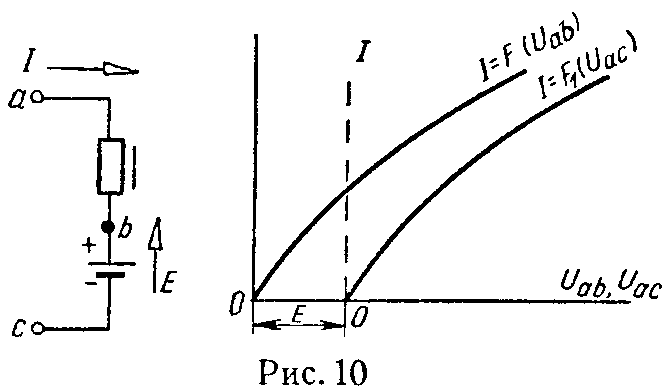

U_ac = U_ab + E.  (9)

При параллельном соединении ветвей, содержащих нелинейный элемент и источник э.д.с., для каждой из ветвей по только что указанному способу строят соответствующие характеристики, затем на их основе, как и в случае параллельного соединения нелинейных элементов, строят характеристику параллельных ветвей (см. п. 2).

При смешанном соединении ветвей, содержащих нелинейные элементы и источники э.д.с., пользуются теми же приемами, как и при смешанном соединении нелинейных элементов (см. п. 2), при этом предварительно строят характеристики для каждой из ветвей, содержащей нелинейный элемент и э.д.с.

5. Расчет токов в сколь угодно сложной цепи, состоящей из любого числа линейных сопротивлений и э.д.с. и содержащей лишь один нелинейный элемент (рис. 11), производится при помощи метода эквивалентного генератора.

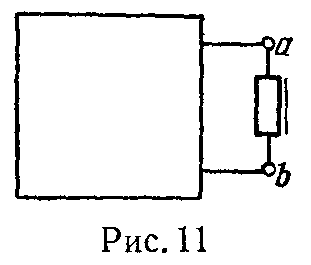
Ветвь ab, содержащая нелинейный элемент, мысленно размыкается, и так же, как в линейных цепях, определяются напряжение холостого хода U_ab = E и сопротивление короткого замыкания r_k по отношению к зажимам ab. На этой основе заданная схема может быть заменена ей эквивалентной согласно рис. 12.

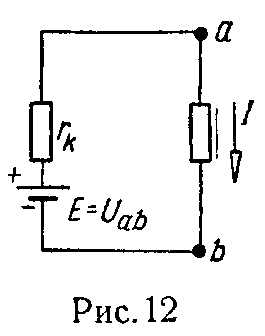
Последняя же может быть рассчитана, как указано выше (п. 2 и 4). Таким образом будет определен ток I в нелинейном элементе. Наконец, возвращаясь к исходной схеме, на основании законов Кирхгофа можно рассчитать токи в остальных ветвях.

Пример — в задаче 20.

---

Упражнения и задачи

Задача 1. Нелинейный элемент имеет вольт-амперную характеристику, уравнение которой

$I=a\cdot U+b\cdot U^3\left(a=8\cdot {10}^{-3}\frac{1}{Ом},b=5\cdot {10}^{-4}\frac{1}{Ом\cdot {В}^2}\right).$

Построить вольт-амперную характеристику элемента. Определить статическое и динамическое сопротивления элемента. Подсчитать значения величин этих сопротивлений для напряжения U_а = 4 В.

Построить кривую зависимости отношения $\frac{r_{ст}}{r_{д}}$  в функции U.

Решение

Вольт-амперная характеристика элемента представляет собой кубическую параболу. Построим ее по точкам следующей таблицы, рассчитанной по заданному уравнению:

Фирма по производству тентов.

Выберем масштабы: для напряжения – $m_U=2\frac{В}{см}$ ; для тока – $m_I=\mathrm{0,05}\frac{А}{см}$ .

По данным таблицы и выбранным масштабам на рис. 13. а построена характеристика I = F (U).

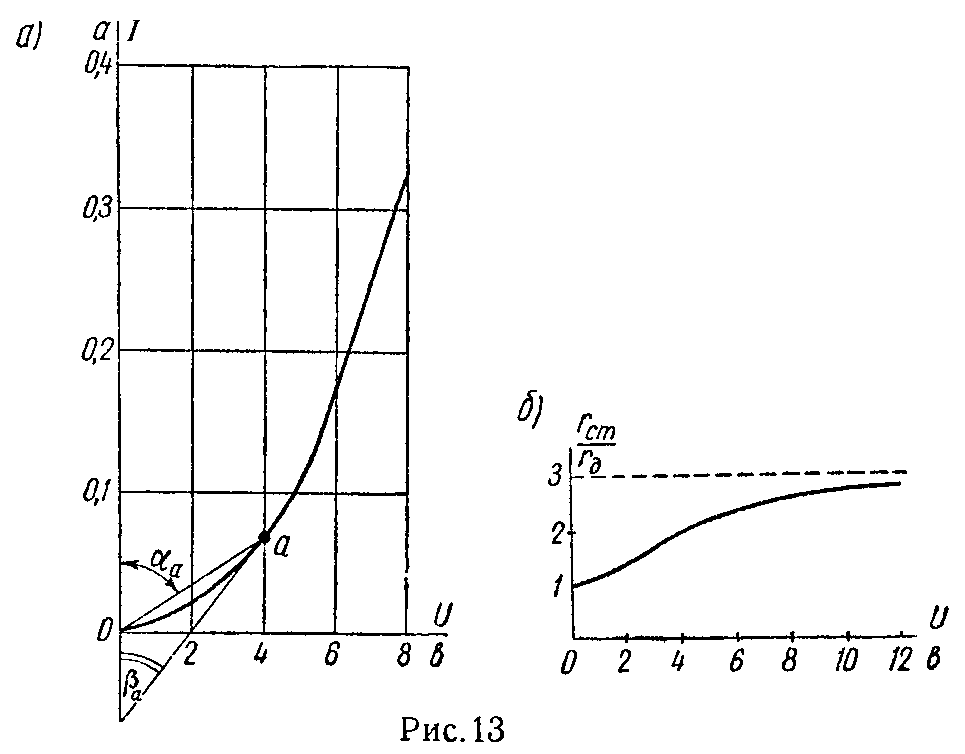
Подсчитаем статическое и динамическое сопротивления по формулам (1) и (2)

$\begin{array}{l}{r}_{ст}=\frac{U}{I}=\frac{U}{aU+b{U}^3}=\frac{1}{a+b{U}^2},\\ r_{д}=\frac{dU}{dI}=\frac{1}{\frac{dI}{dU}}=\frac{1}{a+3b{U}^2}.\end{array}$

Для точки a (U = 4 В)

$\begin{array}{l}{\left(r_{ст}\right)}_a={\left(\frac{1}{a+b{U}^2}\right)}_{U=4}=\frac{1}{8\cdot {10}^{-3}+5\cdot {10}^{-4}\cdot 4^2}=\mathrm{62,5}Ом;\\ {\left(r_{д}\right)}_a={\left(\frac{1}{a+3b{U}^2}\right)}_{U=4}=\frac{1}{8\cdot {10}^{-3}+3\cdot 5\cdot {10}^{-4}\cdot 4^2}=\mathrm{31,25}Ом.\end{array}$

Те же значения можно получить и графическим путем. По формуле (5) вычисляем

$k=\frac{m_U}{m_I}=\frac{2\frac{В}{см}}{\mathrm{0,05}\frac{А}{см}}=40Ом.$

Из рис. 13, а для точки a находим

$\begin{array}{l}tg{\alpha }_a=\frac{20мм}{\mathrm{12,8}мм}=\mathrm{1,5625,}\\ tg{\beta }_a=\frac{20мм}{\mathrm{25,6}мм}=\mathrm{0,78125.}\end{array}$

По формулам (3) и (4) получаем

$\begin{array}{l}{\left(r_{ст}\right)}_a=k\cdot tg{\alpha }_a=40\cdot \mathrm{1,5625}=\mathrm{62,5}Ом;\\ {\left(r_{д}\right)}_a=k\cdot tg{\beta }_a=40\cdot \mathrm{0,78125}=\mathrm{31,25}Ом.\end{array}$

Отношение

$\frac{r_{ст}}{r_{д}}=\frac{a+3b{U}^2}{a+b{U}^2}.$

При U = 0 отношение $\frac{r_{ст}}{r_{д}}=1$ , а при неограниченном увеличении U, пользуясь правилом раскрытия неопределенностей, получим

$\frac{r_{ст}}{r_{д}}=\underset{U\to \infty }{\lim }\frac{a+3b{U}^2}{a+b{U}^2}=\underset{U\to \infty }{\lim }\frac{3b{U}^2}{b{U}^2}=3.$

На рис. 13, б начерчена кривая отношения

$\frac{r_{ст}}{r_{д}}=F\left(U\right).$

---

Задача 2. Дан нелинейный элемент, характеристика которого

$I=a\cdot U^2+2ab\cdot U\left(a=2\cdot {10}^{-3}\frac{1}{Ом\cdot В},b=\mathrm{0,5}В\right).$

Построить характеристику элемента. Найти выражения для r_ст и r_д. Найти значения этих величин для напряжения U = 5 В. Построить кривую $\frac{r_{ст}}{r_{д}}=F\left(U\right).$

Ответ: $r_{ст}=\frac{500}{U+1},r_{д}=\frac{250}{U+\mathrm{0,5}};$  при U = 5 В: r_ст = 83,3 Ом, r_д. = 45,5 Ом.

---

Задача 3. Ток кенотрона (в пределах от нуля до тока насыщения) в зависимости от анодного напряжения (при постоянстве напряжения накала) выражается уравнением, получившим название «закона степени трех вторых»,

$I_a=g\cdot U_a^{3/2},$

где коэффициент g зависит от формы и размеров электродов и для данной лампы является постоянной величиной.

Начертить вольт-амперную характеристику. Вычислить крутизну характеристики S в точке, соответствующей анодному напряжению 200 В.

Чему равно внутреннее сопротивление лампы постоянному и переменному токам при том же напряжении, т.е. статическое и динамическое сопротивления лампы.

Коэффициент g принять равным $\mathrm{0,07}\cdot {10}^{-3}\frac{1}{Ом\cdot {В}^{1/2}}.$

Указание. Крутизной характеристики в заданной точке называется отношение приращения анодного тока к приращению анодного напряжения, т.е.

$S=\frac{d{I}_a}{d{U}_a}.$

Крутизна характеристики — величина обратная динамическому сопротивлению.

Решение

Начертим вольт-амперную характеристику (рис. 14) на основе данных следующей таблицы, рассчитанной по уравнению

$I_a=7\cdot {10}^{-5}\cdot U_a^{3/2}:$

Крутизна характеристики

$S=\frac{d{I}_a}{d{U}_a}=\frac{d}{d{U}_a}\left(g\cdot U_a^{3/2}\right)=\frac{3}{2}g\cdot U_a^{1/2}.$

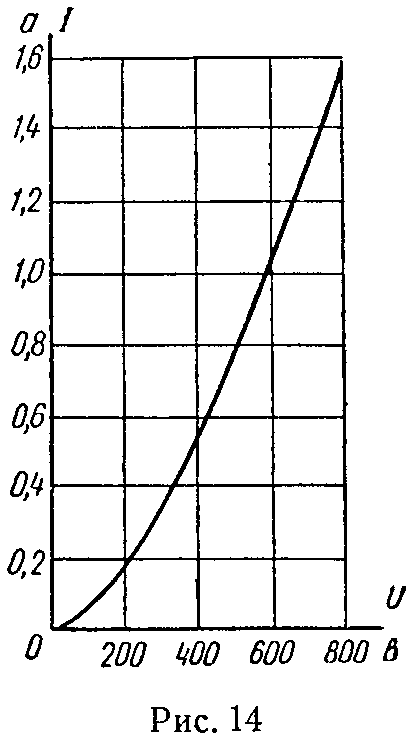
Вычислим ее значение в точке, требуемой условиями задачи

$S_{U_a=200}={\left[\frac{3}{2}g\cdot U_a^{1/2}\right]}_{U_a=200}=\frac{3}{2}\cdot \mathrm{0,07}\cdot {10}^{-3}\cdot {200}^{1/2}=\mathrm{1,49}\cdot {10}^{-3}\frac{А}{В}=\mathrm{1,49}\frac{мА}{В}.$

Внутреннее сопротивление лампы постоянному току (статическое сопротивление)

Внутреннее сопротивление лампы изменению тока (динамическое сопротивление)

$$\begin{array}{l}{r}_{д}=\frac{d{U}_a}{d{I}_a}=\frac{1}{\frac{d{I}_a}{d{U}_a}}=\frac{2}{3g\cdot U_a^{1/2}},\\ {\left(r_{д}\right)}_{U_a=200}={\left[\frac{2}{3g\cdot U_a^{1/2}}\right]}_{U_a=200}=\frac{2}{3\cdot 7\cdot {10}^{-5}\cdot \sqrt{200}}=675Ом.\end{array}$$

---

Задача 4. Даны нелинейное сопротивление r₁ (I₁) вольт-амперная характеристика которого

$I_1=a\cdot U_1^2\left(a=\mathrm{0,02}\frac{1}{Ом\cdot В}\right),$

и линейное сопротивление r₂ = 12 Ом.

Определить ток, протекающий в цепи, и напряжение на каждом сопротивлении при их последовательном соединении и включении на постоянное напряжение U = 4 В (рис. 15, а).

Задачу решить аналитически и графически.

Решение

1) Аналитическое решение. Приложенное к цепи напряжение

U = U₁ + U₂,

где U₁ — напряжение на нелинейном элементе, причем I₁ = a·U₁², U₂ — напряжение на линейном сопротивлении (U₂ = I₂·r₂). Учитывая, что при последовательном соединении сопротивлений ток во всех элементах цепи имеет одинаковое значение I = I₁ = I₂, можно записать

U = U₁ + U₂ = U₁ + I·r₂ = U₁ + a·r₂·U₁²

или

a·r₂·U₁² + U₁ — U = 0,

или после подстановки чисел

0,24·U₁² + U₁ — 4 = 0.

Решая квадратное уравнение получим

U₁ = 2,5 В.

Второе, отрицательное значение корня отбрасываем, как лишенное физического смысла.

Теперь найдем искомые величины

I = a·U₁² = 0,02·2,5² = 0,125 А,

U₂ = I·r₂ = 0,125·12 = 1,5 В.

2) Графическое решение. Первый способ. Вначале по точкам, рассчитанным по уравнению I₁ = a·U₁², построим вольт-амперную характеристику нелинейного элемента:

Выберем масштабы: для напряжения m_U = 1 В/см, для тока — m_I = 0,5 А/см.

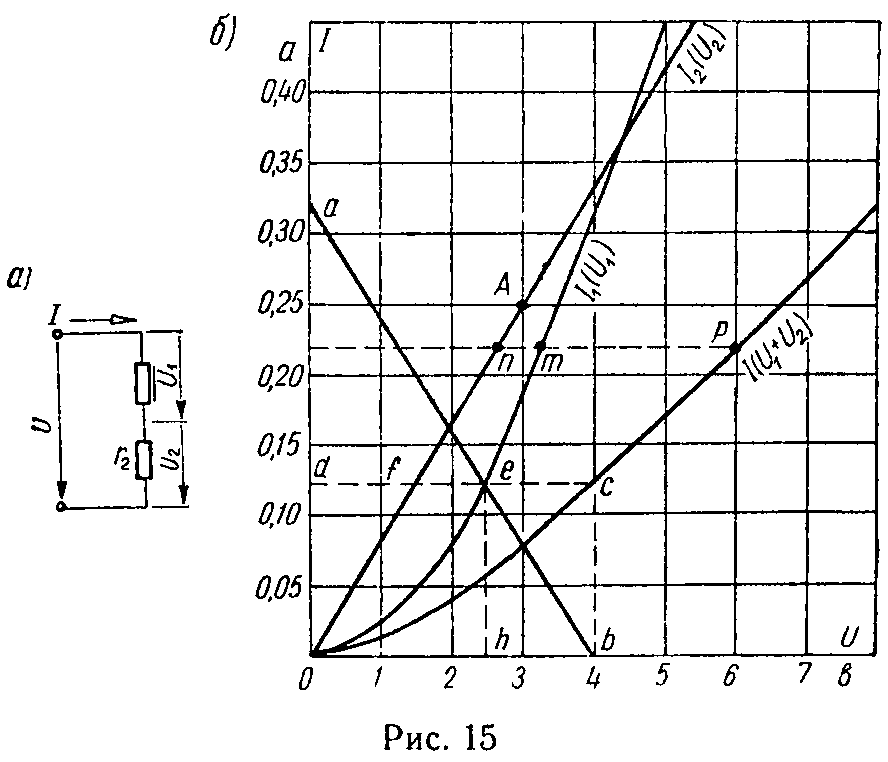
На рис. 15, б построена кривая I₁ (U₁) = a·U₁². Теперь построим вольт-амперную характеристику линейного сопротивления r₂. График этой зависимости I₂ (U₂) = U₂/r₂ = U₂/12 выражен прямой, проходящей через начало координат, тангенс угла наклона которой к оси абсцисс равен 1/12. Проще всего эту прямую построить так: зададимся любым значением U₂, например, U₂ = 3 В, и подсчитаем соответствующее значение I₂ = U₂/r₂ = 3/12 = 0,25 А; полученную таким образом точку А соединяем прямой с началом координат. Это и будет нанесенная на рис. 15, б прямая I₂ (U₂).

Затем построим вольт-амперную характеристику зависимости тока I в функции общего напряжения U₁ + U₂. Так как ток в обоих элементах имеет одно и то же значение, то для построения характеристики I в зависимости от U₁ + U₂ просуммируем напряжения U₁ и U₂ для одних и тех же значений тока. Для этого через ординаты, соответствующие 0,05 А; 0,10 А; 0,15 А …, проводим прямые, параллельные оси U, и для каждого значения тока откладываем соответствующие значения абсцисс. Таким образом, получим результирующую кривую I (U₁ + U₂). На рис. 15, б показано построение для одной точки I = 0,225 А, при этом U₁ = 3,36 В (дочка m), U₂ = 2,7 В (точка n) и общее напряжение

U = U₁ + U₂ = 6,06 В (точка p).

Теперь на основании проведенных построений можно ответить на вопросы, поставленные в условии задачи. Для этого отложим на оси абсцисс отрезок ab, соответствующий напряжению U = 4 В, и из точки b проводим прямую, параллельную оси ординат, до пересечения ее с кривой I (U₁ + U₂) в точке c. Отрезок bc дает в выбранных масштабах искомый ток I = 0,125 А. Наконец, проводя из точки c прямую cd, параллельную оси абсцисс, найдем искомые напряжения: отрезок de дает напряжение на нелинейном элементе U₁ = 2,5 В, отрезок df — напряжение на сопротивлении r₂: U₂ = 1,5 В.

Второй способ. При расчете цепи по этому способу нет необходимости строить результирующую характеристику всей схемы. По закону Ома имеем

U₁ + I·r₂ = U.

Это уравнение перепишем в виде

U₁ = U — I·r₂.  (1)

Левая часть последнего уравнения определяет вольт-амперную характеристику нелинейного элемента — кривая I₁ (U₁) на рис. 15, б, а правая — прямую ab, отсекающую на оси абсцисс отрезок 0b, равный U, и наклоненную к ней под углом, тангенс которого равен отношению отрезков 0a к 0b умноженному на отношение масштаба тока m_I к масштабу напряжения m_U, т. е.

$\frac{Oa\cdot m_I}{Ob\cdot m_U}=-\frac{1}{r_2}=-\frac{1}{12}.$

Иными словами, прямая ab является опрокинутой характеристикой линейного элемента относительно вертикали, проходящей через точку b. Очевидно, что точка e пересечения прямой ab с вольт-амперной характеристикой удовлетворяет уравнению (1). Ордината точки e в соответствующем масштабе дает искомый ток (отрезок eh соответствует 0,125 А).

---

Задача 5. Последовательно с нелинейным сопротивлением r₁ (I) (лампа с угольной нитью), вольт-амперная характеристика которого представлена на рис. 16, включено линейное сопротивление r₂ = 40 Ом.

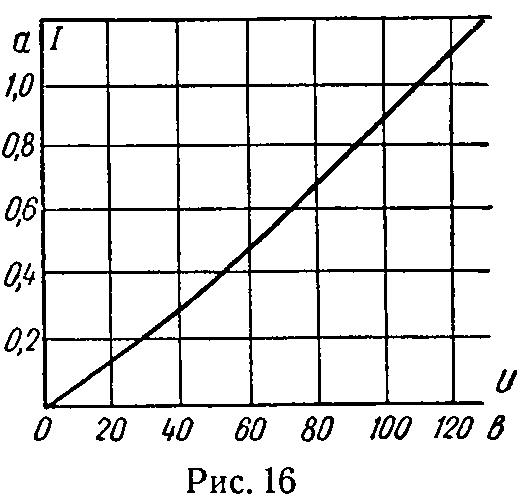
а) Определить ток, протекающий в цепи при подключении к схеме напряжения U = 115 В. Каково при этом напряжение на лампе U₁ и напряжение U₂ на линейном сопротивлении?

б) При каком напряжении на зажимах цепи напряжение на лампе будет U₂ = 60 В?

в) Какое напряжение надо подключить к цепи, чтобы напряжение на линейном сопротивлении было в 2,5 раза меньше, чем на лампе?

г) Чему равно статическое сопротивление схемы в случаях «а», «б», «в»?

Ответ: а) 0,72 А; U₁ = 85 В; U₂ = 30 В, б) 80 В, в) 29 В, г) для «а» 118 Ом; для «б» 125 Ом; для «в» 138 Ом.

---

Задача 6. Нелинейное сопротивление r₁ (I₁) вольт-амперная характеристика которого $I_1=a\cdot U_1^2\left(a=\mathrm{0,02}\frac{1}{Ом\cdot В}\right),$  и линейное сопротивление r₂ = 25 Ом соединены параллельно; при этом в неразветвленном участке цепи проходит ток I = 225 мА. Определить, какое напряжение U подключено к цепи и чему равны токи, протекающие через каждое из сопротивлений (рис. 17, а).

Задачу решить аналитически и графически.

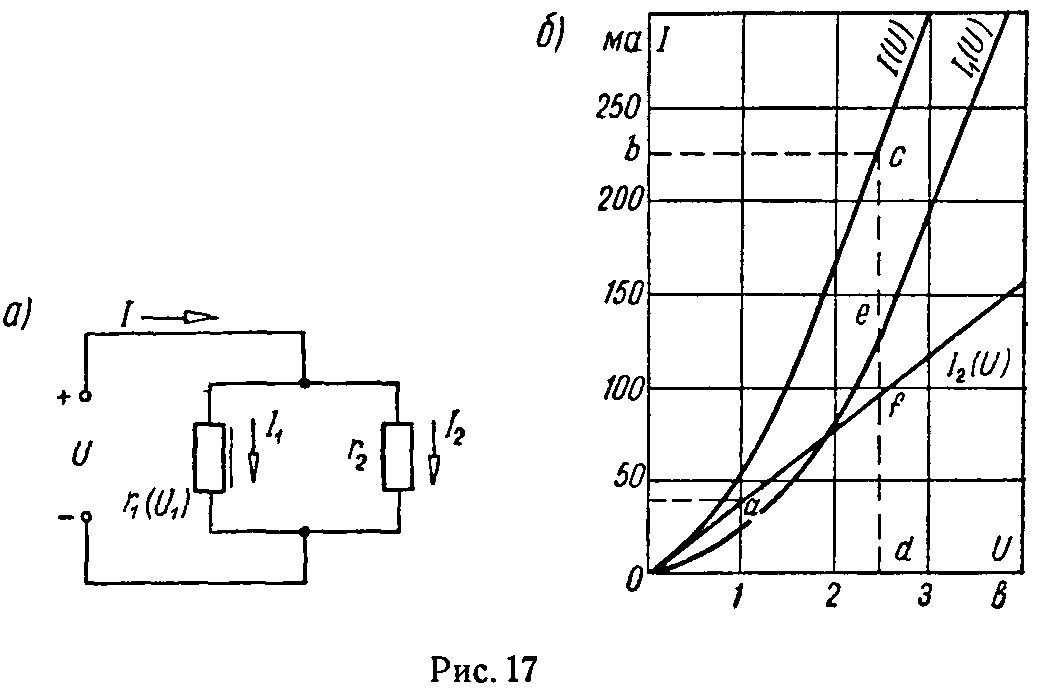
Решение

1) Аналитическое решение. На основании первого закона Кирхгофа имеем

I = I₁ + I₂ = a·U² + U/r₂,

или после подстановки числовых значений

0,02U² + 0,04U — 0,225 = 0.

Решая полученное квадратное уравнение, найдем искомое напряжение U = 2,5 В.

Второй корень (отрицательный) отбрасываем, как не удовлетворяющий смыслу задачи.

При найденном напряжении токи в отдельных ветвях равны

I₁ = a·U² = 0,02·2,5² = 0,125 А;

I₂ = U/r₂ = 2,5/25 = 0,1 А.

2) Графическое решение. Построим характеристику нелинейного элемента по данным следующей таблицы, рассчитанным по уравнению I₁ = a·U²:

Для построения характеристики выберем масштабы: напряжений — m_U = 1 В/см, для тока — m_I = 50 мА/см. Далее, по уравнению I₂ (U₂) = U₂/r₂ = U₂/25 построим вольт-амперную характеристику I₂ (U) линейного сопротивления r₂. Для этого зададимся произвольным значением U, например, равным 1 В, тогда соответствующее значение тока I₂ (U₂) = U₂/r₂ = 1/25 = 0,04 А = 40 мА.

Характеристика I₂ (U) пройдет через начало координат и точку a, абсцисса которой соответствует 1 В и ордината — 40 мА. Наконец, по уравнению первого закона Кирхгофа I₁ (U) + I₂ (U) = I (U) строим характеристику I (U), выражающую зависимость тока в неразветвленной части цепи I от напряжения U (рис. 17, б). Для этого суммируем ординаты I₁ (U) и I₂ (U), соответствующие одинаковым абсциссам.

Чтобы определить напряжение, приложенное к схеме, из точки b (отрезок 0b соответствует току 225 мА) проводим прямую bc, параллельную оси абсцисс; из точки c опускаем перпендикуляр cd на ось абсцисс. Отрезок 0d соответствует искомому напряжению U = 2,5 В, отрезок de — току I₁ =125 мА и отрезок df — току I₂ = 100 мА (df + de = dc).

---

Задача 7. Параллельно с нелинейным сопротивлением r₁ (I₁) (лампа с вольфрамовой нитью), вольт-амперная характеристика которого представлена на рис. 18, а, соединено линейное сопротивление r₂ = 180 Ом (рис. 18, б).

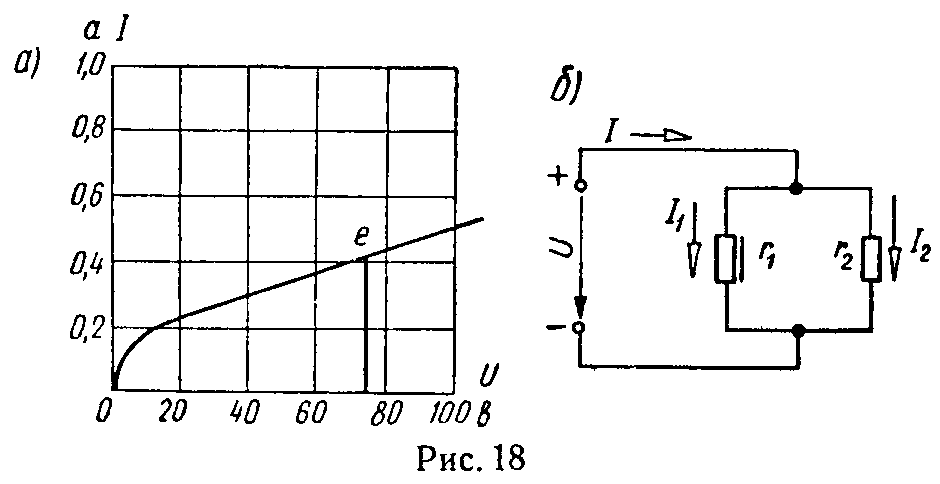
а) Построить зависимость тока I, протекающего в неразветвленной части цепи, от приложенного напряжения U.

б) Определить токи, протекающие через каждую из параллельных ветвей, если ток в неразветвленной части цепи равен 0,6 А.

в) При каком значении напряжения ток, протекающий через линейное сопротивление, равен току, протекающему через лампу; чему равен этот ток?

г) При каком значении приложенного напряжения ток, протекающий через линейное сопротивление, будет в 2 раза меньше, чем ток, протекающий через лампу?

д) Чему равно эквивалентное статическое сопротивление схемы в случаях «б», «в» и «г»?

Ответ: б) 0,336 А и 0,264 А, в) 0,416 А при 75 В, г) 23 В, д) для «б» 79,2 Ом; для «в» 180 Ом; для «г» 60 Ом.

---

Задача 8. Вольт-амперная характеристика тиритового диска выражается уравнением I = 2,13·10^–10·U^3,5 (I — в амперах, U — в вольтах).

Подобрать линейное сопротивление r, подключаемое параллельно к тиритовому диску так, чтобы при напряжении U = 550 В ток в неразветвленной части цепи равнялся I = 1 А.

Тиритовые элементы используются в нелинейных мостовых схемах автоматики, в защитных устройствах при передаче энергии высоким напряжением. Тирит — керамическое вещество, основу которого составляет мелкоизмельченный графит и карборунд, подвергнутые определенной термической обработке.

Решение

Определим ток, протекающий через тиритовый диск при заданном напряжении.

Пусть

x = 550^3,5,

тогда

tgx = 3,5·lg550 = 3,5·2,74036 = 9,59126,

x = 3,9·10⁹.

Ток

I = 2,13·10^–10·550^3,5 = 2,13·10^–10·3,9·10⁹ = 0,83 А.

Ток, проходящий через       линейное сопротивление, будет равен

1,0 — 0,83 = 0,17 А.

Искомое сопротивление

r = 550/0,17 ≈ 3240 Ом.

---

Задача 9. Какое сопротивление надо включить последовательно с тиритовым элементом, вольт-амперная характеристика которого I = 3,1·10^–8·U^3,5 (I — в амперах, U — в вольтах), для того, чтобы при напряжении генератора, подключенного к цепи U = 120 В, в ней проходил ток I = 0,22 А.

Вычислить, какая мощность будет при этом расходоваться в тиритовом элементе и в сопротивлении r.

Решение

Найдем напряжение U₁ на тиритовом элементе при заданном токе I

0,22 = 3,1·10^–8·U₁^3,5,

или

U₁^3,5 = 0,22·10⁸/3,1;

логарифмируя, получим

3,5·lgU₁ = lg (7,1·10⁶) = 6,85126;

или

lgU₁ = 6,85126/3,5 = 1,9575,

отсюда

U₁ = 90,7 В.

По закону Ома U = U₁ + I·r, откуда

$r=\frac{U-U_1}{I}=\frac{120-\mathrm{90,7}}{\mathrm{0,22}}=133Ом.$

Мощность, расходуемая в тиритовом элементе

P₁ = U₁I₁ = 90,7·0,22 = 19,95 Вт.

Мощность, расходуемая в сопротивлении

P₂ = I²r = 0.22²·133 = 6,45 Вт.

---

Задача 10. Для измерительных цепей собрана цепь (рис. 19, а), состоящая из двух линейных сопротивлений r₁ = 100 Ом и r = 20 Ом и меднозакисного выпрямителя, характеристика которого в проводящем направлении имеет вид, представленный кривой 1 на рис. 19, б.

Найти все токи и напряжения на сопротивлениях r₁ и r₂, если цепь подключена к напряжению U = 1,4 В.

Определить при этом напряжении эквивалентное сопротивление цепи и сопротивление нелинейного элемента r₂.

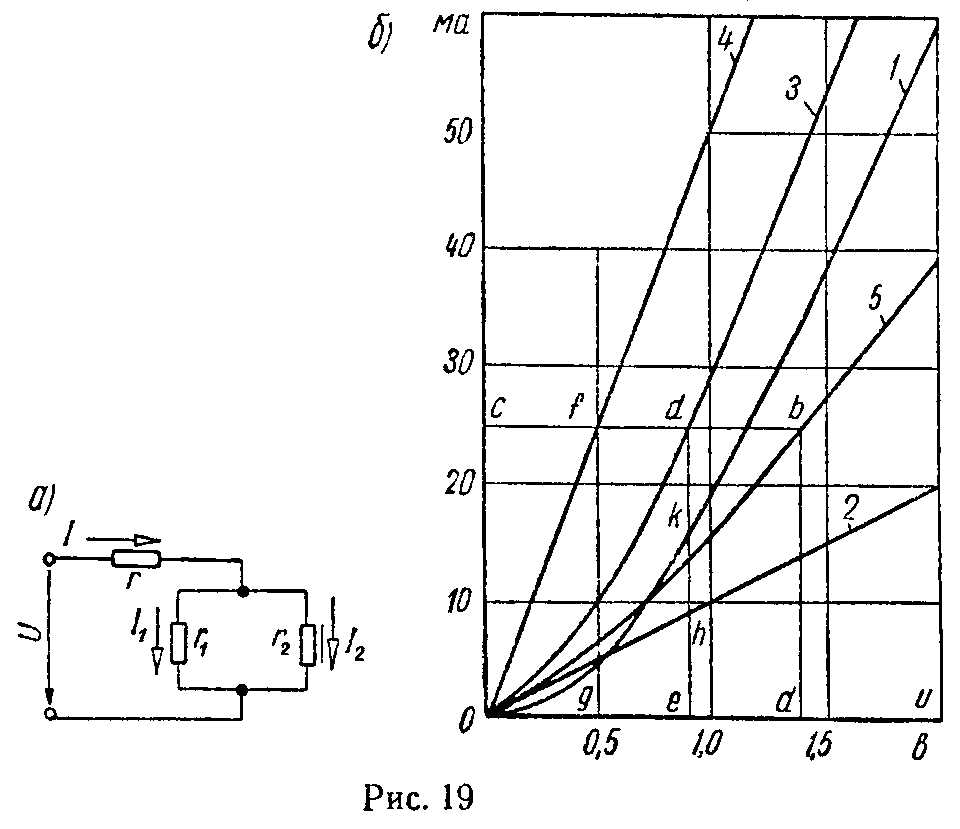
Решение

На рис. 19, б построены: характеристика выпрямителя — кривая 1, характеристика сопротивления r₁ — прямая 2, характеристика параллельного участка цепи — кривая 3 (ее ординаты являются суммами соответствующих ординат кривой 1 и прямой 2); затем построены: характеристика сопротивления r — прямая 4 и характеристика всей цепи — кривая 5. Абсциссы кривой 5 равны суммам соответствующих абсцисс кривой 3 и прямой 4. Через точку a, соответствующую заданному напряжению U = 1,4 В, проводим ординату до пересечения ее с кривой 5 в точке b. Отрезок 0c выражает собой ток I = 25 мА. Через точки d и f пересечения прямой bc с кривыми 3 и 4 опускаем перпендикуляры de и fg на ось абсцисс. Отрезок 0g, соответствующий 0,5 В, выражает собой напряжение на сопротивлении r, а отрезок 0e, соответствующий 0,9 В, выражает напряжение на параллельных ветвях цепи. Отрезки eh и ek выражают собой токи, протекающие через линейное и нелинейное сопротивления, соответственно равные 9 и 16 мА.

Проверка дает

U = I·r + I₁·r₁ = 0,025·20 + 0,009·100 = 1,4 В.

Определим эквивалентное сопротивление цепи

$r_{э}=\frac{U}{I}=\frac{\mathrm{1,4}}{\mathrm{0,025}}=56Ом.$

Сопротивление нелинейного элемента

$r_2=\frac{U_2}{I_2}=\frac{\mathrm{0,9}}{\mathrm{0,016}}=56\mathrm{,25}Ом.$

Таким образом, эквивалентное сопротивление цепи

$r_{э}=r+\frac{r_1\cdot r_2}{r_1+r_2}=20+\frac{100\cdot \mathrm{56,25}}{100+\mathrm{56,25}}=20+36=56Ом.$

---

Задача 11. Электронная лампа работает в электрической цепи, схема которой приведена на рис. 20, а.

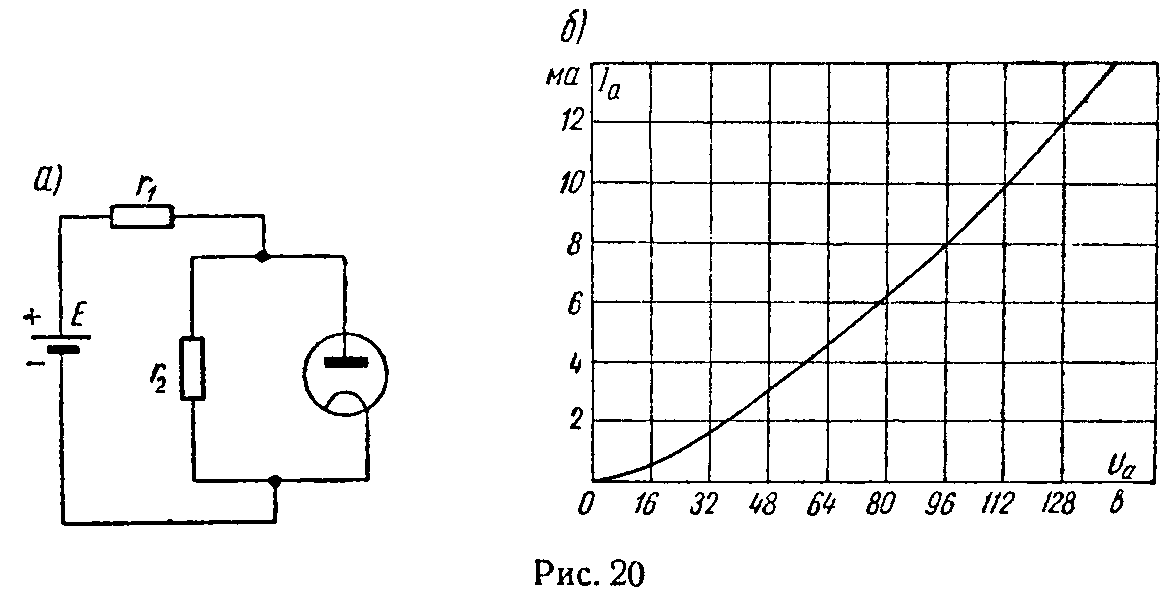
Анодная характеристика лампы (т.е. зависимость анодного тока лампы от напряжения анода, при неизменных напряжениях других электродов) дана на рис. 20, б.

Определить ток в лампе, если r₁ = 2 кОм, r₂ = 24 кОм, E = 120 В.

Ответ: 8 мА.

---

Задача 12. Цепь состоит из линейного сопротивления r = 5 Ом, последовательно с которым соединены два включенных параллельно друг другу нелинейных элемента, вольт-амперные характеристики которых

$\begin{array}{l}{I}_1=a_1\cdot U_1^2+b\cdot U_1\left(a_1=\mathrm{0,02}\frac{1}{Ом\cdot В},b=\mathrm{0,01}\frac{1}{Ом}\right),\\ I_2=a_2\cdot U_2^2\left(a_2=\mathrm{0,03}\frac{1}{Ом\cdot В}\right).\end{array}$

Определить ток, протекающий в каждой ветви, если к цепи приложено напряжение U = 7,8 В.

Задачу решить аналитически и графически.

Ответ: 0,28 А, 0,48 А.

---

Задача 13. Для поддержания постоянства тока в цепи накала электронной лампы (r_н), питаемой от аккумуляторной батареи (U = 24 В), применен барретер типа Б-3. Определить, чему должны быть равны сопротивления r₁ и r₂, включаемые как показано на рис. 21, а, если напряжение на нити накала U₁ = 6,3 В, а ток нити накала I₁ = 0,7 А.

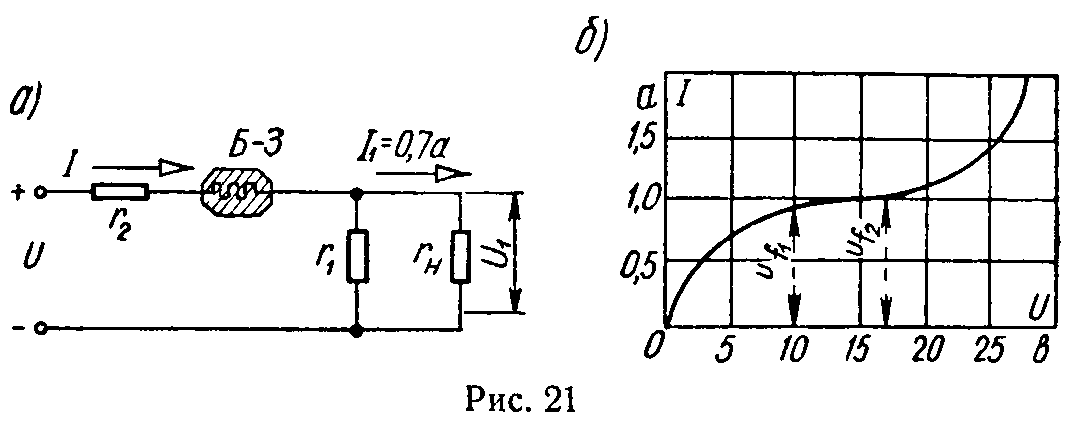
Границы участка, на котором значение тока поддерживается практически стабильным, определяются следующими величинами: U_fl = 10 В, I_fl = 0,97 А; U_f2 == 17 В, I_f2 = 1,03 А. На рис. 21, б представлена зависимость тока от напряжения для барретера типа Б-3.

Барретер (бареттер) представляет собой заполненный водородом стеклянный баллон, внутрь которого помещена тонкая платиновая, железная или вольфрамовая проволока (нить).

Принцип действия состоит в том, что при увеличении приложенного напряжения возрастает температура нити накала и, следовательно, ее сопротивление. В результате при изменении напряжения на бареттере сила тока практически не изменяется. Таким образом, бареттер, включенный последовательно с нагрузкой, поддерживает в ней стабильный ток при изменениях напряжения питания.

Решение

По условию задачи применен барретер, рассчитанный на стабилизацию тока в 1 А, т.е. через сопротивление r₂, включенное последовательно с барретером, должен проходить ток, равный 1 А. Этот ток распределяется по двум параллельным ветвям, причем, согласно условию, в цепи накала лампы (r_н) протекает ток, равный 0,7 А; следовательно, через параллельно включенное к нити накала лампы сопротивление r₁ должен проходить ток, равный 1 — 0,7 = 0,3 А. Напряжение на сопротивлении r₁ таково же, как и на нити накала, U₁ = 6,3 В, следовательно,

r₁ = 6,3/0,3 = 21 Ом.

Для получения наиболее широкой области стабилизации целесообразно выбрать рабочую точку посредине участка характеристики барретера, на котором значение тока практически постоянно; этой точке соответствует напряжение барретера

U_б = (10 + 17)/2 = 13, 5 В.

По второму закону Кирхгофа

U = I·r₂ + U_б + U₁.

Откуда

$r_2=\frac{U-U_{б}-U_1}{I}=\frac{24-\mathrm{13,5}-\mathrm{6,3}}{1}=\mathrm{4,2}Ом.$

---

Задача 14. Мост собран из двух линейных сопротивлений r по 100 Ом каждое и из двух одинаковых тиритовых элементов Т, вольт-амперная характеристика которых

$I_1=M\cdot U_T^m,$

где $M=\mathrm{3,1}\cdot {10}^{-8}\frac{1}{Ом\cdot {В}^{\mathrm{2,5}}},m=\mathrm{3,5}$  (I₁ — в амперах, U — в вольтах).

Одинаковые элементы включены в противолежащие ветви моста (рис. 22).

Найти, чему должно быть равно напряжение, к которому подключен мост для того, чтобы ток в диагонали моста был равен нулю.

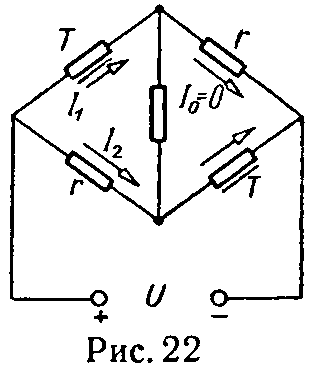
Решение

При заданной схеме равновесие моста требует, чтобы сопротивление тиритового элемента равнялось r_Т = r.

Из характеристики

$r_T=\frac{U_T}{I_1}=\frac{U_T}{M\cdot U_T^m}=\frac{1}{M\cdot U_T^{m-1}}=r,$

откуда напряжение на тиритовом элементе

$U_T=\sqrt[m-1]{\frac{1}{r\cdot M}}=\sqrt[\mathrm{2,5}]{\frac{1}{100\cdot \mathrm{3,1}\cdot {10}^{-8}}}=160В=\frac{1}{2}U,$

отсюда искомое напряжение моста

U = 2·160 = 320 В.

---

Задача 15. Решить задачу 14 в случаях, если сопротивление будет равно: а) r = 80 Ом, б) r = 120 Ом.

Ответ: а) 350 В, б) 300 В.

---

Задача 16. Найти распределение токов и напряжений в цепи (рис. 23, а) при U = 12 В. Вольт-амперные характеристики нелинейных элементов r₁ (I₁) и r₂ (I₂) представлены на рис. 23, б. Линейное сопротивление r₃ = 150 Ом.

Задачу решить методом линеаризации (см. п. 3), при этом следует исходить из того, что в рассматриваемом режиме рабочие участки вольт-амперных характеристик могут быть представлены прямыми:

для нелинейного сопротивления r₁ (I₁)

U₁ = I₁·r_д1 — E₁,

для нелинейного сопротивления r₂ (I₂)

U₂ = I₂·r_д2 + E₂,

при

$\begin{array}{l}{r}_{д1}=\frac{d{U}_1}{d{I}_1}=380Ом,E_1=12В,\\ r_{д2}=\frac{d{U}_2}{d{I}_2}=30Ом,E_1=\mathrm{1,8}В.\end{array}$

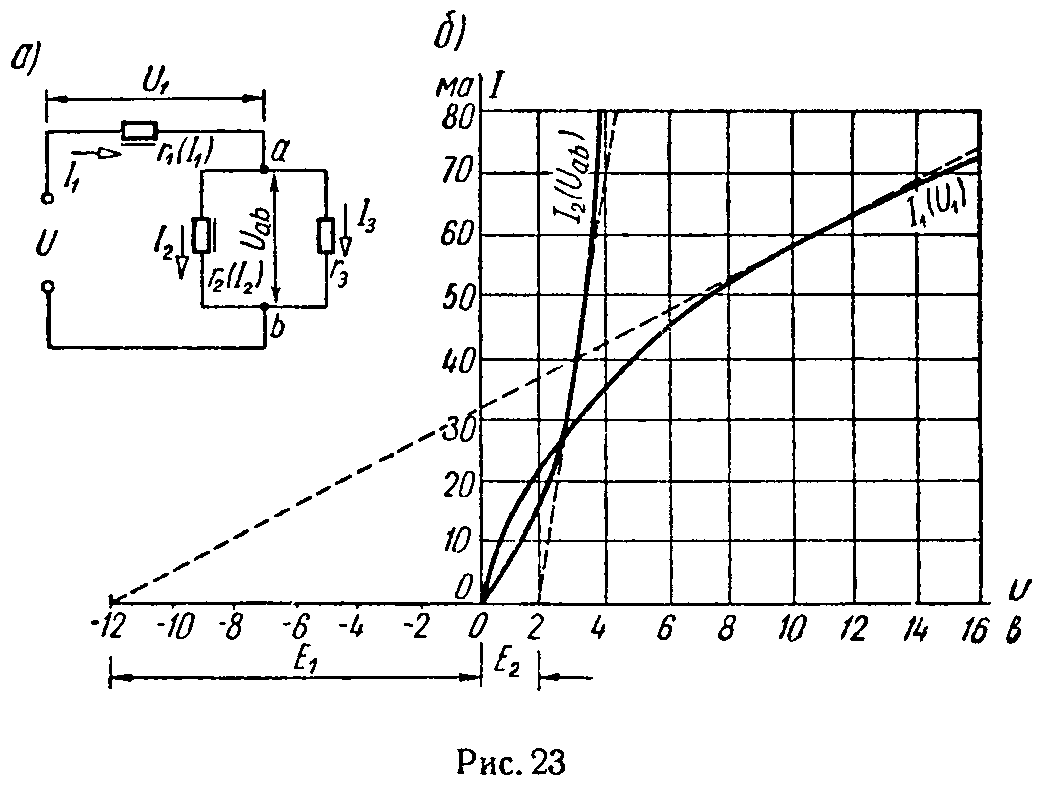
Решение

Искомые токи и напряжения с учетом заданных аналитических выражений для U₁ можно определить из следующих уравнений

U = U₁ + U_ab = I₁·r_д1 — E₁ + I₂·r_д2 + E₂, (1)

I₃·r₃ = I₂·r_д2 + E₂,  (2)

I₁ + I₂·= I₃.  (3)

Решаем эти уравнения совместно. Для этого подставляем значение I₃ из (3) во (2) и из полученного уравнения находим

$I_1=\frac{E_2}{r_3}+I_2\frac{r_{д2}+r_3}{r_3}.$   (4)

Подставляя I₁ в уравнение (1), получим

$I_2=\frac{U\cdot r_3-E_2\cdot r_{д1}+E_1\cdot r_3-E_2\cdot r_3}{r_{д1}\cdot r_{д2}+r_3\cdot r_{д1}+r_3\cdot r_{д2}}.$   (5)

Подставляя сюда числовые значения, найдем

I₂ = 36,2 мА,

а затем из (4), после подстановки чисел,

I₁ = 55,5 мА

и, наконец, из (3)

I₃ = 19,3 мА.

Теперь определим напряжения на отдельных участках цепи. Из уравнения (2)

U_ab = I₃·r₃ = 2,9 В,

а из уравнения (1)

U₁ = U — U_ab = 12 — 2,9 = 9,1 В.

Осуществим проверку того, что найденные величины соответствуют выбранным участкам. Действительно, обращаясь к характеристикам рис. 23, б, видим, что найденные значения для токов лежат в пределах линеаризированных участков. Следовательно, расчет правилен.

Рекомендуем читателю решить задачу графическим путем.

---

Задача 17. Воспользовавшись данными задачи 16, ответить на вопросы, поставленные в ней в случаях: 1) U = 13 В, 2) U = 14 В.

Ответ:  1) U₁ = 10,05 В, U₂ = 2,95 В, I₁ = 58 мА, I₂ = 38,3 мА, I₃ = 19,7 мА;

---

Задача 18. Определить напряжение на линейных элементах схемы, 24, а и токи в ветвях, если напряжение U_АВ = 25 В, E₁ = 15 В, E₂ = 10 В.

Вольт-амперные характеристики нелинейных элементов представлены на рис. 24, б.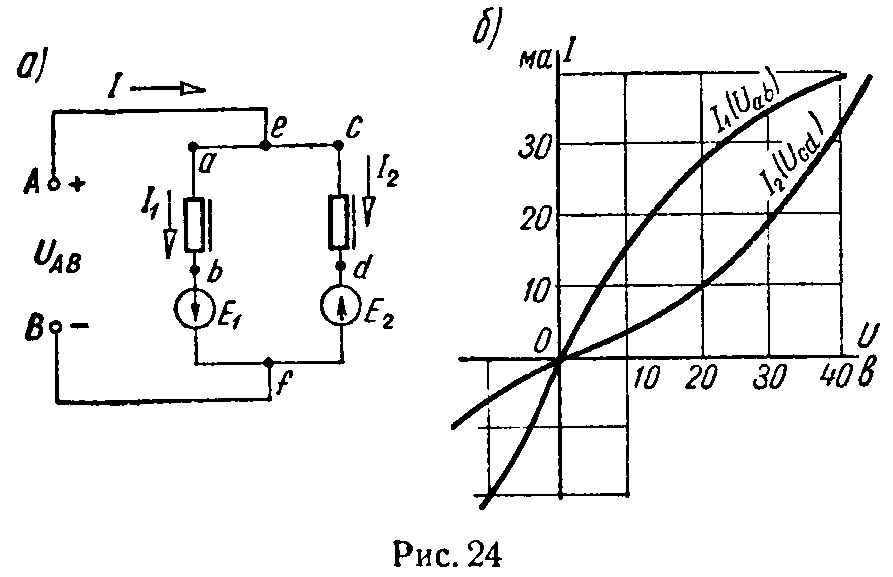

Ответ: U_ab = 40 В, I₁ = 38 мА, U_cd = 15 В, I₂ = 7 мА.

---

Задача 19. В схеме рис. 25, содержащей два одинаковых нелинейных элемента, определить все токи, если E₁ = 2 В, E₂ = 3 В при значениях: а) U_АВ = 5 В, б) U_АВ = 1 В.

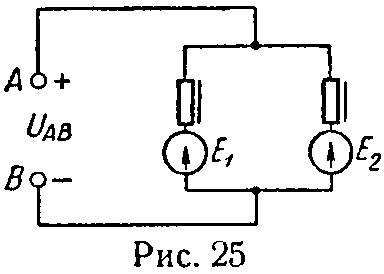
Вольт-амперные характеристики каждого из элементов

$I=a\cdot U+b\cdot U^3\left(a=8\cdot {10}^{-3}\frac{1}{Ом},b=5\cdot {10}^{-4}\frac{1}{Ом\cdot {В}^2}\right).$

Ответ: а) I = 57,5 мА, I₁ = 37,5 мА, I₂ = 20 мА; б) I = 28,5 мА, I₁ = 8,5 мА, I₂ = 20 мА.

---

Задача 20. Рассчитать токи в схеме, изображенной на рис. 26, а. Вольт-амперная характеристика нелинейного сопротивления r₆ (I₆) приведена на рис. 26, б.

Электродвижущие силы E₁ = 12 В, E₂ = 23 В; линейные сопротивления r₁ = 250 Ом, r₂ = 150 Ом, r₃ = 700 Ом, r₄ = 100 Ом, r₅ = 50 Ом. Внутренние сопротивления источников э. д. с. принять равными нулю.

Решение

Задача решается в соответствии с указаниями, данными в п. 5. Размыкаем ветвь с нелинейным сопротивлением r₆ и методом эквивалентного генератора (см. Линейные электрические цепи постоянного тока п. 4 Метод эквивалентного генератора напряжения) определяем напряжение холостого хода U_ab = E_х (рис. 26, в) и сопротивление короткого замыкания по отношению к зажимам ac (рис. 26, г).

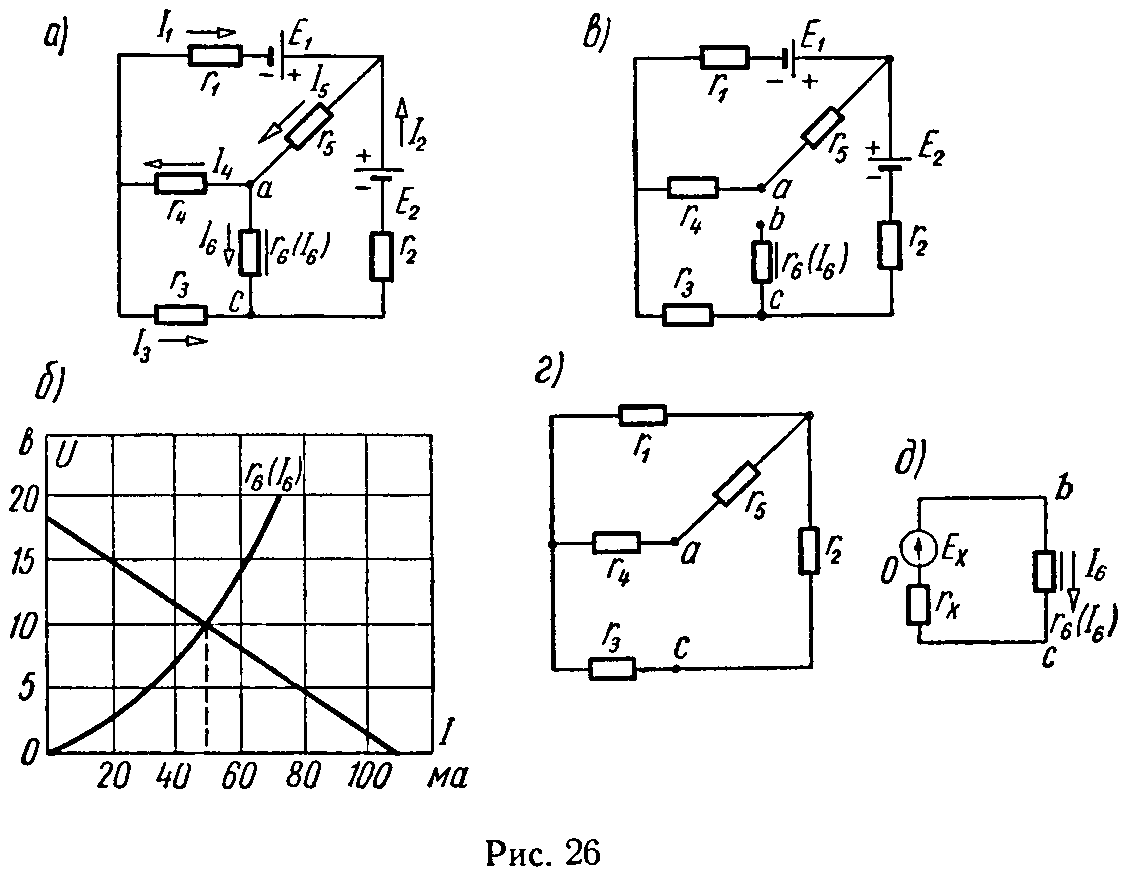
Расчеты дают U_ab = E_х ≈ 18 В, r_k = 160 Ом (предлагается читателю проделать эти расчеты самостоятельно).

Заданная схема может быть заменена ей эквивалентной, согласно рис. 26, д. Ток в ней может быть определен графически, как показано в п. 2.

По уравнению U_bc = E_х — I₆·r_k = 18 — 160·I₆ на рис. 26, б построена прямая, выражающая зависимость U_bc = f (I₆). Абсцисса точки ее пересечения с заданной вольт-амперной характеристикой нелинейного сопротивления r₆ (I₆) определяет искомый ток I₆ = 0,05 А; при этом U_ac = 10 В. Остальные токи находятся путем применения законов Кирхгофа (рис. 26, а):

E_l = I₁·r₁ + I₅·r₅ + I₄·r₄,

E₂ = I₂·r₂ + I₅·r₅ + U_ас,

U_ас = I₄·r₄ + I₃·r₃,

I₁ + I₂ — I₅ = 0,

I₄ — I₁ — I₃ = 0.

Совместное решение этих уравнений дает:

I₁ = 0,02 А, I₂ = 0,06 А, I₃ = 0,01 А, I₄ = 0,03 А, I₅ = 0,08 А.

---

Задача 21. В схеме рис. 27, а рассчитать токи.

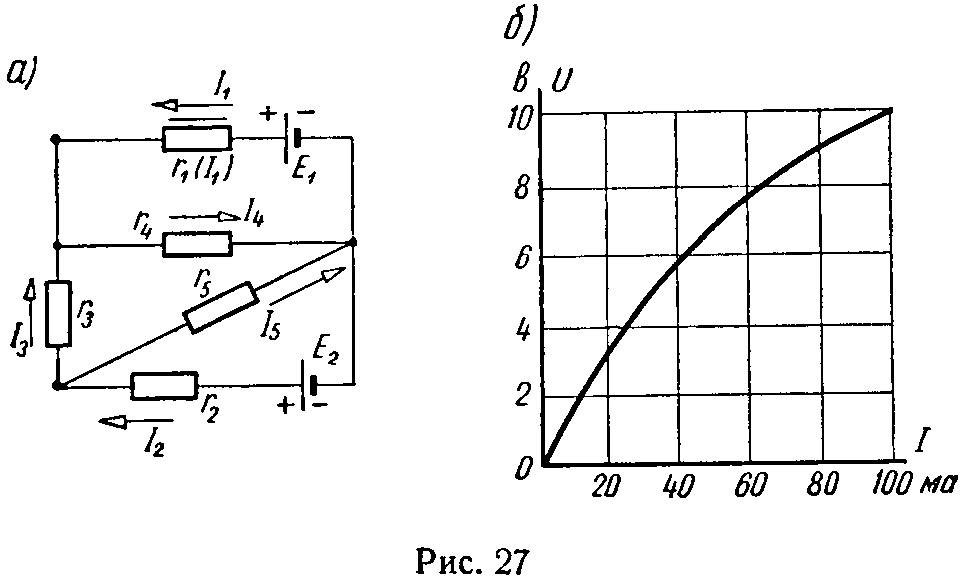
Даны: E₁ = 10 В, E₂ = 14 В, r₂ = 50 Ом, r₃ = 100 Ом, r₄ = 40 Ом, r₅ = 500 Ом, вольт-амперная характеристика сопротивления r₁ (I₁) приведена на рис. 27, б.

Ответ: I₁ = 0,04 А, I₂ = 0,08 А, I₃ = 0,06 А, I₄ = 0,1 А, I₅ = 0,02 А.

---

---

дифференциальное сопротивление, кусочно-линейная аппроксимация, графический метод расчета нелинейных электрических цепей, динамическое сопротивление, статическое сопротивление, ВАХ нелинейного элемента, вольт-амперная характеристика нелинейного элемента, нелинейный элемент