Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 3 Методы расчета линейных цепей синусоидального тока → 3.4 Цепи со взаимными индуктивностями

3.4 Цепи со взаимными индуктивностями

Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 3 Методы расчета линейных цепей синусоидального тока

3.4 Цепи со взаимными индуктивностями

В цепях с взаимной индуктивностью появляется новая разновидность составляющих напряжения, обусловленная ЭДС взаимной индукции. В связи с этим расчет цепей с взаимной индукцией несколько сложней расчета цепей аналогичной конфигурации без взаимной индукции

---

Задача 3.4.1 Найти показания ваттметров в схеме рис. 3.4.1, а, рассчитать передаваемую активную мощность магнитным полем, построить векторную диаграмму напряжений и токов, если U = 150 + j150 В, R₁ = 5 Ом, R₂ = 10 Ом, ωL₁ = 15 Ом, ωL₂ — 1/(ωC₂) = 0, ωM = 10 Ом.

Показать, что схема рис. 3.4.1, б, является эквивалентной схемой замещения данной цепи без магнитных связей.

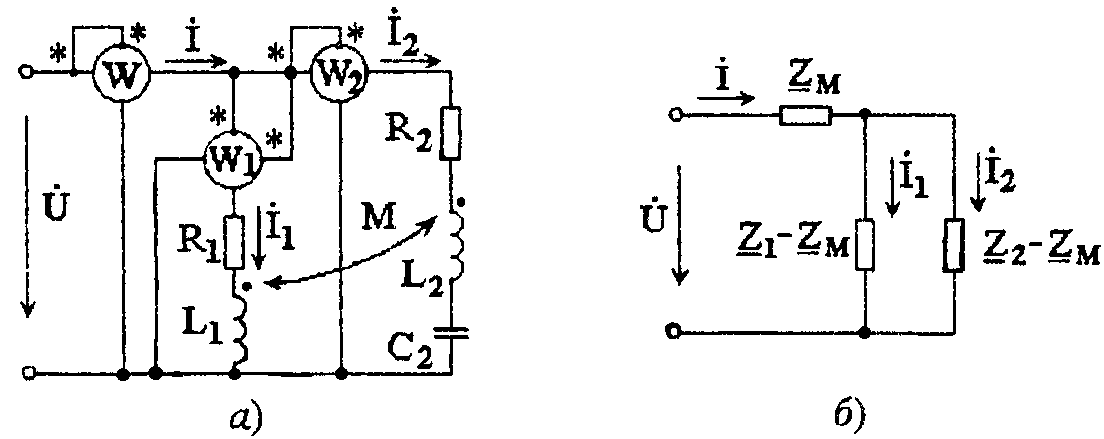
Рис. 3.4.1 а) схема цепи с магнитными связями; б) эквивалентная схема замещения цепи без магнитных связей

Решение. Составляем систему уравнений по законам Кирхгофа для цепи по схеме рис. 3.4.1, а

$\{\begin{array}{l}\stackrel{?}{I}={\stackrel{?}{I}}_1+{\stackrel{?}{I}}_2;\\ {\stackrel{?}{I}}_1{\underset{\_}{Z}}_1+{\stackrel{?}{I}}_2{\underset{\_}{Z}}_M=\stackrel{?}{U};\\ {\stackrel{?}{I}}_1{\underset{\_}{Z}}_M+{\stackrel{?}{I}}_2{\underset{\_}{Z}}_2=\stackrel{?}{U}.\end{array}$

Очевидно, что при соответствующей замене тока ${\stackrel{?}{I}}_2=\stackrel{?}{I}-{\stackrel{?}{I}}_1$  и тока ${\stackrel{?}{I}}_1=\stackrel{?}{I}-{\stackrel{?}{I}}_2$  мы приходим к системе уравнений

$\{\begin{array}{l}\stackrel{?}{I}={\stackrel{?}{I}}_1+{\stackrel{?}{I}}_2;\\ \stackrel{?}{I}{\underset{\_}{Z}}_M+{\stackrel{?}{I}}_1\left({\underset{\_}{Z}}_1-{\underset{\_}{Z}}_M\right)=\stackrel{?}{U};\\ \stackrel{?}{I}{\underset{\_}{Z}}_M+{\stackrel{?}{I}}_2\left({\underset{\_}{Z}}_2-{\underset{\_}{Z}}_M\right)=\stackrel{?}{U},\end{array}$

которой соответствует схема рис. 3.4.1, б.

В приведенных системах комплексные сопротивления определяются выражениями

$\begin{array}{l}{\underset{\_}{Z}}_1=R_1+j\omega L_1=5+j15Ом;\\ {\underset{\_}{Z}}_2=R_2+j\left(\omega L_2-\frac{1}{\omega C_2}\right)=10Ом;\\ {\underset{\_}{Z}}_M=j\omega M=j10Ом.\end{array}$

Соответствующие значения токов равны

${\stackrel{?}{I}}_1=10-j10А;{\stackrel{?}{I}}_2=5+j5А;\stackrel{?}{I}=15-j5А.$

Показания ваттметров

$\begin{array}{l}P=\mathrm{Re}\left[\stackrel{?}{U}\stackrel{*}{I}\right]=\mathrm{Re}\left[\left(150+j150\right)\left(15+j5\right)\right]=1500Вт;\\ P_1=\mathrm{Re}\left[\stackrel{?}{U}{\stackrel{*}{I}}_1\right]=\mathrm{Re}\left[\left(150+j150\right)\left(10+j10\right)\right]=0Вт;\\ P_2=\mathrm{Re}\left[\stackrel{?}{U}{\stackrel{*}{I}}_2\right]=\mathrm{Re}\left[\left(150+j150\right)\left(5-j5\right)\right]=1500Вт.\end{array}$

Активная мощность, передаваемая из второй ветви в первую,

$P_{21}=\mathrm{Re}\left[{\stackrel{?}{I}}_{1}j{X}_M{\stackrel{*}{I}}_2\right]=\mathrm{Re}\left[\left(10-j10\right)\cdot j10\cdot \left(5-j5\right)\right]=1000Вт$

или

$P_{21}=P_2-I_2^2{R}_2=1500-500=1000Вт.$

Векторная диаграмма токов и напряжений приведена на рисунке 3.4.2.

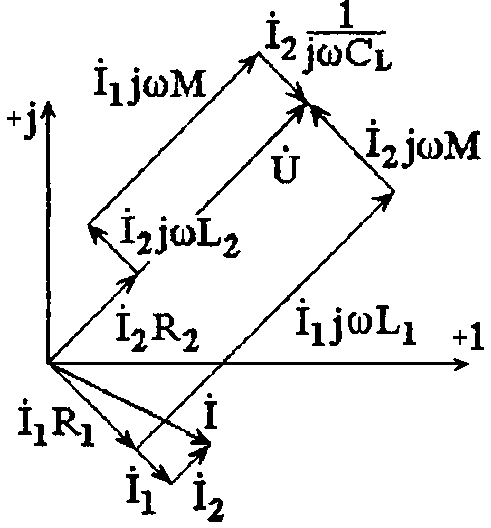
Рис. 3.4.2 Векторная диаграмма токов и напряжений

Задача 3.4.2 Определить E и построить топографическую диаграмму схемы рис. 3.4.3, приняв потенциал φ₄ = 0, если 1/(ωC) = 35 Ом, ωL₁ = 20 Ом, ωL₂ = 60 Ом, ωM = 10 Ом, R = 20 Ом, I₂ = 1 А.

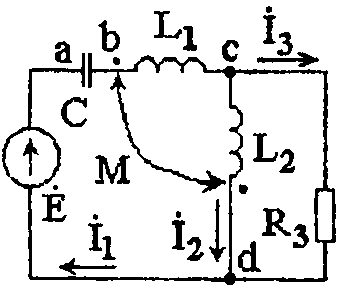
Рис. 3.4.3 Схема цепи с индуктивной связью

Решение

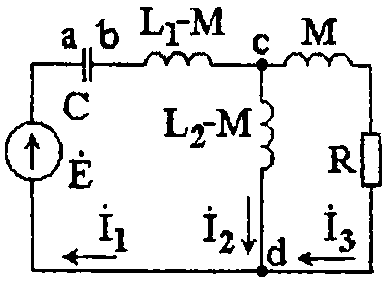
Рис. 3.4.4 Эквивалентная схема замещения цепи с развязанной индуктивной связью

Произведя развязку индуктивной связи, получим эквивалентную схему (рис. 3.4.4), для которой

$\begin{array}{l}{\stackrel{?}{I}}_3=\frac{{\stackrel{?}{U}}_{cd}}{R+j{X}_M}=\frac{{\stackrel{?}{I}}_2\cdot j\left(\omega L_2-\omega M\right)}{R+j\omega M}=\frac{1\cdot j\left(60-10\right)}{20+j10}=1+j2А;\\ {\stackrel{?}{I}}_1={\stackrel{?}{I}}_2+{\stackrel{?}{I}}_3=1+\left(1+j2\right)=2+j2А;\\ \stackrel{?}{E}={\stackrel{?}{I}}_1\cdot j\left(\omega L_1-\omega M-\frac{1}{\omega С}\right)+{\stackrel{?}{I}}_2\cdot j\left(\omega L_2-\omega M\right)=\\ =\left(2+j2\right)\cdot j\left(20-10-35\right)+1\cdot j\left(60-10\right)=50В.\end{array}$

Для построения топографической диаграммы рассчитаем потенциалы в схеме рис. 3.4.3

$$\begin{array}{l}{\stackrel{?}{\phi }}_c={\stackrel{?}{\phi }}_d+{\stackrel{?}{I}}_3{R}_3=0+\left(1+j2\right)\cdot 20=20+j40В;\\ {\stackrel{?}{\phi }}_b={\stackrel{?}{\phi }}_c+{\stackrel{?}{I}}_1\cdot j\omega L_1-{\stackrel{?}{I}}_2\cdot j\omega M=\\ =\left(20+j40\right)+\left(2+j2\right)\cdot j20-1\cdot j10=-20+j70В;\\ {\stackrel{?}{\phi }}_a=\stackrel{?}{E}={\stackrel{?}{\phi }}_b+{\stackrel{?}{I}}_1\cdot \left(-j\frac{1}{\omega C}\right)=\left(-20+j70\right)+\left(2+j2\right)\cdot \left(-j35\right)=50В.\end{array}$$

Топографическая диаграмма приведена на рис. 3.4.5.

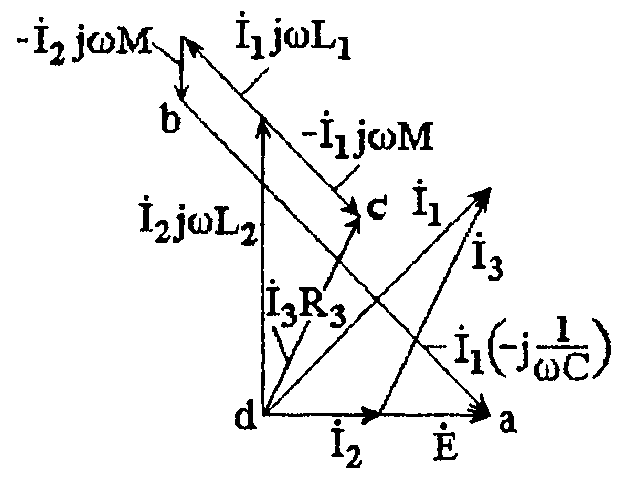
Рис. 3.4.5 Топографическая диаграмма

Задача 3.4.3 На кольцевой сердечник, изготовленный из неферромагнитного материала, намотаны три катушки с активными сопротивлениями R_l = R₂ = R₃ = 5 Ом и с индуктивными сопротивлениями X₁ = ωL₁ = 10 Ом, X₂ = ωL₂ = 20 Ом и X₃ = ωL₃ = 15 Ом. Сопротивления, обусловленные взаимными индуктивностями между соответствующими парами катушек, заданы равными

X₁₂ = X₂₁ = ωM₁₂ = 10 Ом,

X₁₃ = X₃₁ = ωM₁₃ = 10 Ом,

X₂₃ = X₃₂ = ωM₂₃ = 15 Ом.

Ветви с первой и второй катушками соединены между собой параллельно. Напряжение на их зажимах U =200 В. Во вторую ветвь дополнительно включен конденсатор с сопротивлением (при заданной частоте) Х_2С = 20 Ом. Третья катушка замкнута на конденсатор с сопротивлением Х_3С = 15 Ом.

Определить токи во всех ветвях, составить уравнение баланса активных мощностей для всей цепи.

Указание к решению задачи и ответ. Согласно условию самостоятельно изобразите содержание поставленной задачи. Докажите, что в результате можно прийти к следующей электрической схеме замещения (рис. 3.4.6).

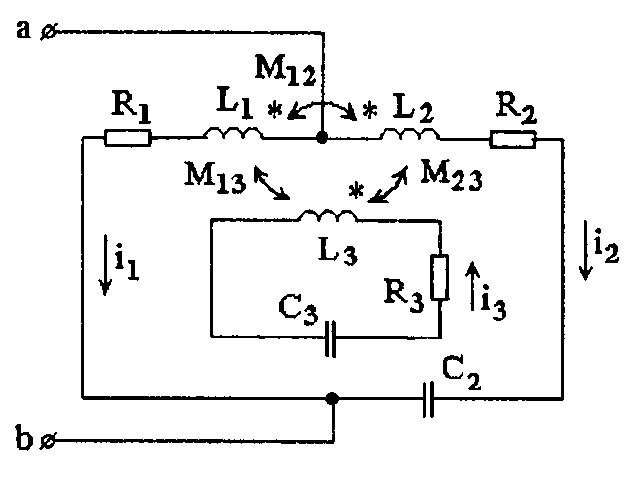
Рис. 3.4.6 Электрическая схема замещения кольцевого сердечника

Токи в ветвях определяются из уравнений

$\begin{array}{l}\stackrel{?}{U}={\underset{\_}{Z}}_1{\stackrel{?}{I}}_1+j{X}_{12}{\stackrel{?}{I}}_2+j{X}_{13}{\stackrel{?}{I}}_3;\\ \stackrel{?}{U}={\underset{\_}{Z}}_2{\stackrel{?}{I}}_2+j{X}_{21}{\stackrel{?}{I}}_1+j{X}_{23}{\stackrel{?}{I}}_3;\\ 0={\underset{\_}{Z}}_3{\stackrel{?}{I}}_3+j{X}_{31}{\stackrel{?}{I}}_1+j{X}_{32}{\stackrel{?}{I}}_2.\end{array}$

В результате совместного решения этих уравнений получаем

$\begin{array}{l}{\stackrel{?}{I}}_1=\stackrel{?}{U}\frac{{\underset{\_}{Z}}_{2Э}-{\underset{\_}{Z}}_{12}}{{\underset{\_}{Z}}_{1Э}{\underset{\_}{Z}}_{2Э}-{\underset{\_}{Z}}_{12}{\underset{\_}{Z}}_{21}};\\ {\stackrel{?}{I}}_2=\stackrel{?}{U}\frac{{\underset{\_}{Z}}_{1Э}-{\underset{\_}{Z}}_{21}}{{\underset{\_}{Z}}_{1Э}{\underset{\_}{Z}}_{2Э}-{\underset{\_}{Z}}_{12}{\underset{\_}{Z}}_{21}};\\ {\stackrel{?}{I}}_3=-j\frac{X_{31}}{R_3}{\stackrel{?}{I}}_1-j\frac{X_{32}}{R_3}{\stackrel{?}{I}}_2,\end{array}$

где

$\begin{array}{l}{\underset{\_}{Z}}_{1Э}={\underset{\_}{Z}}_1+\frac{X_{31}^2}{R_3};\\ {\underset{\_}{Z}}_{2Э}={\underset{\_}{Z}}_2+\frac{X_{23}^2}{R_3};\\ {\underset{\_}{Z}}_{12}={\underset{\_}{Z}}_{21}=j{X}_{12}+\frac{X_{13}{X}_{32}}{R_3}.\end{array}$

Подставляя заданные значения параметров в выражения для токов, получим

$\begin{array}{l}{\stackrel{?}{I}}_1=\mathrm{9,4}-j\mathrm{2,35}А;\\ {\stackrel{?}{I}}_2=-\mathrm{2,12}-j\mathrm{0,47}А;\\ {\stackrel{?}{I}}_3=-\mathrm{6,11}-j\mathrm{12,44}А.\end{array}$

Уравнение баланса активных мощностей для рассматриваемой цепи запишется в следующем виде

$P_{ист}=P_{потр},$

где

$\begin{array}{l}{P}_{ист}=\mathrm{Re}\left(\stackrel{?}{U}\cdot \stackrel{*}{I}\right)=\mathrm{Re}\left[\stackrel{?}{U}\cdot \left({\stackrel{*}{I}}_1+{\stackrel{*}{I}}_2\right)\right];\\ P_{потр}=I_1^2{R}_1+I_2^2{R}_2+I_3^2{R}_3.\end{array}$

---

взаимная индуктивность