Контактные данные

Решение задач ТОЭ

Решение ТОЭ онлайн

Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях → 1.2 Метод наложения

1.2 Метод наложения

Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях

1.2 Метод наложения

Метод наложения основан на свойстве линейности электрических цепей. Метод наложения справедлив только для линейных цепей. Метод наложения применяется для определения токов в ветвях схемы с несколькими источниками.

Алгоритм метода наложения:

1) выбирают положительные направления токов в ветвях цепи;

2) находят частичные токи в ветвях, вызванные каждым источником по отдельности (схему рассчитывают столько раз, сколько источников действует в схеме);

3) токи в ветвях по методу наложения находят как алгебраическую сумму частичных токов (знак частичного тока при суммировании определяется по положительному направлению тока ветви).

Решение задач методом наложения

Задача 1.2.1. В электрической цепи рис. 1.2.1 с тремя источниками энергии определить все токи в ветвях, воспользовавшись методом наложения.

Свадьба в Челябинске.

Задача 1.2.1. В электрической цепи с тремя источниками энергии определить все токи в ветвях, воспользовавшись методом наложения

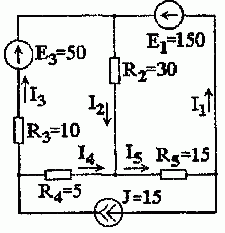
Рис. 1.2.1

Решение

1. Выполним расчет цепи при воздействии источника ЭДС E₁, полагая E₃ = 0, J = 0. Источники считаем идеальными, поэтому внутренние сопротивления ЭДС равны нулю, а источника тока — бесконечности. С учетом этого изобразим расчетную схему (рис. 1.2.2).

Рисунок 1.2.2 Часчетная схема частичных токов от ЭДС E1

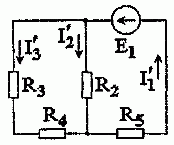
Рис. 1.2.2

Увлекательные встречи с красивыми и умными девушками доступны на сайте https://volgodonsksm.com для всех желающих.

Определение токов в полученной схеме будем вести, пользуясь методом эквивалентных преобразований:

$\begin{array}{l} {R^{'}}_{Э} = R_{5} + \frac{R_{2} \cdot (R_{3} + R_{4})}{R_{2} + (R_{3} + R_{4})} = 15 + \frac{30 \cdot (10 + 5)}{30 + (10 + 5)} = 25 О м; \\ {I^{'}}_{1} = \frac{E_{1}}{{R^{'}}_{Э}} = \frac{150}{25} = 6 A; {I^{'}}_{5} = {I^{'}}_{1} = 6 A; \\ {I^{'}}_{2} = {I^{'}}_{1} \cdot \frac{R_{3} + R_{4}}{R_{2} + (R_{3} + R_{4})} = 6 \cdot \frac{10 + 5}{30 + (10 + 5)} = 6 A; \\ {I^{'}}_{3} = {I^{'}}_{1} \cdot \frac{R_{2}}{R_{2} + (R_{3} + R_{4})} = 6 \cdot \frac{30}{30 + (10 + 5)} = 4 A; {I^{'}}_{3} = {I^{'}}_{4} = 4 A . \end{array}$

2. Расчет электрической цепи при воздействии ЭДС источника Е₃ выполним, полагая Е₁ = 0, J = 0 (рис. 1.2.3).

Рисунок 1.2.3 Расчетная схема частичных токов от ЭДС E3

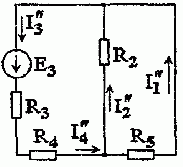
Рис. 1.2.3

В соответствии с рис. 1.2.3 имеем:

$\begin{array}{l} {R^{″}}_{Э} = R_{3} + R_{4} + \frac{R_{2} \cdot R_{5}}{R_{2} + R_{5}} = 10 + 5 + \frac{30 \cdot 15}{30 + 15} = 25 О м; \\ {I^{″}}_{3} = \frac{E_{3}}{{R^{″}}_{Э}} = \frac{50}{25} = 2 A; {I^{″}}_{4} = {I^{″}}_{3} = 2 A; \\ {I^{″}}_{2} = {I^{″}}_{4} \cdot \frac{R_{5}}{R_{2} + R_{5}} = 2 \cdot \frac{15}{15 + 30} = 0,66 A; \\ {I^{″}}_{5} = {I^{″}}_{4} \cdot \frac{R_{2}}{R_{2} + R_{5}} = 2 \cdot \frac{30}{15 + 30} = 1,33 A; {I^{″}}_{1} = {I^{″}}_{5} = 1,33 A . \end{array}$

3. Расчет электрической цепи при действии источника тока выполним, полагая E₁ = 0, Е₂ = 0 (рис. 12.4).

Рисунок 1.2.4 Частичные токи в цепи от источника тока

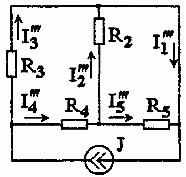
Рис. 1.2.4

В соответствии с рис. 1.2.4 имеем:

${R^{?}}_{Э} = R_{4} + \frac{R_{2} \cdot R_{5}}{R_{2} + R_{5}} = 5 + \frac{30 \cdot 15}{30 + 15} = 15 О м .$

Находим токи в параллельных ветвях:

$\begin{array}{l} {I^{?}}_{3} = J \cdot \frac{{R^{?}}_{Э}}{{R^{?}}_{Э} + R_{3}} = 15 \cdot \frac{15}{15 + 10} = 9 A; \\ {I^{?}}_{4} = J \cdot \frac{R_{3}}{{R^{?}}_{Э} + R_{3}} = 15 \cdot \frac{10}{15 + 10} = 6 A; \\ {I^{?}}_{2} = {I^{?}}_{4} \cdot \frac{R_{5}}{R_{2} + R_{5}} = 6 \cdot \frac{15}{15 + 30} = 2 A; \\ {I^{?}}_{5} = {I^{?}}_{4} \cdot \frac{R_{2}}{R_{2} + R_{5}} = 6 \cdot \frac{30}{15 + 30} = 4 A . \end{array}$

Ток $I^{?}$ рассчитываем по первому закону Кирхгофа:

${I^{?}}_{1} + {I^{?}}_{5} - J = 0; {I^{?}}_{1} = J - {I^{?}}_{5} = 15 - 4 = 11 A .$

4. В соответствии с принятыми направлениями токов в исходной схеме определим их значения по методу наложения как алгебраическую сумму частичных токов всех промежуточных расчетных схем:

$\begin{array}{l} I_{1} = {I^{'}}_{1} + {I^{″}}_{1} - {I^{?}}_{1} = 6 + 1,33 - 11 = - 3,67 A; \\ I_{2} = {I^{'}}_{2} - {I^{″}}_{2} - {I^{?}}_{2} = 2 - 0,66 - 2 = - 0,66 A; \\ I_{3} = - {I^{'}}_{3} - {I^{″}}_{3} + {I^{?}}_{3} = - 4 - 2 + 9 = 3 A; \\ I_{4} = {I^{'}}_{4} + {I^{″}}_{4} + {I^{?}}_{4} = 4 + 2 + 6 = 12 A; \\ I_{5} = {I^{'}}_{5} + {I^{″}}_{5} + {I^{?}}_{5} = 6 + 1,33 + 4 = 11,33 A . \end{array}$

Правильность решения задачи проверяем по первому закону Кирхгофа:

$\begin{array}{l} - J + I_{3} + I_{4} = 0; - 15 + 3 + 12 = 0; \\ - I_{2} - I_{4} + I_{5} = 0; - (- 0,66) - 12 + 11,33 = 0. \end{array}$

Токи I₁ и I₂ получились отрицательными, т.е. их истинное направление в схеме противоположно принятому положительному направлению.

Метод наложения в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

метод наложения, частичные токи

Комментарии

Метод наложения

Как это в узнали R ′ Э = R 5 + R 2 ⋅ (R 3 + R 4) R 2 + (R 3 + R 4) и это I ′ 2 = I ′ 1 ⋅ R 3 + R 4 R 2 + (R 3 + R 4) ?оъясните

Это эквивалентное сопротивление цепи относительно зажимов ЭДС Е1. Нашли методом свертки последовательно или параллельно включенных резисторов.

Илья · #

Эквивал сопр

Почему в R```Э не учитывается R3? Эквивалентное сопротивление находим для R4+R2||R5 -это одна ветвь, а вторая ветвь — R3.

Виталий · #

Возможно опечатка

В нахождеии конечного тока I3 возможно опечатка, мне кажется что знаки должны быть +I3'-I3''+i3'' Ответ. Спасибо. Изменил направление тока I3' на рис. 1.2.2.

Andre · #

Заказать решение ТОЭ

Новости

Контактные данные

1.2 Метод наложения

Метки