Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 2 Магнитное поле и магнитные цепи при постоянных токах → 2.2 Катушки и трансформаторы со стальными сердечниками

2.2 Катушки и трансформаторы со стальными сердечниками

Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 2 Магнитное поле и магнитные цепи при постоянных токах

Катушки и трансформаторы со стальными сердечниками

Основные положения и соотношения

1. Цепь со сталью представляет собой электрическую цепь, магнитный поток которой полностью или частично заключен в одном или нескольких сердечниках.

Особенности цепей со сталью:

а) нет прямой пропорциональности между магнитным потоком Ф и током i; это приводит к искажению форм кривых тока и э.д.с.; индуктивность не является постоянной величиной и зависит от силы тока.

Уравнение

$$u=i\cdot r+L\frac{di}{dt},$$

справедливое для катушек без стального сердечника, должно быть заменено уравнением

$$u=i\cdot r+\frac{d\Psi }{dt}=i\cdot r-e=i\cdot r+e^{\prime },$$

где ЭДС самоиндукции

$$e=-\frac{d\Psi }{dt}.$$

Действующее значение э.д.с., индуктированной в катушке, определяется при помощи уравнения

E = 4,44·f·w·Ф_m,  (1)

где Ф_m — амплитудное значение магнитного потока;

б) замыкание потока через сталь связано при переменном токе с затратой энергии, превращаемой в тепло.

2. Потери в стали. Потери мощности на магнитный гистерезис определяются по формуле

$\frac{P}{G}=\alpha \cdot B_m\cdot \frac{f}{100}+\beta \cdot B_m^2\cdot \frac{f}{100}.$   (2)

Для индукций в пределах от 1 до 1,6 Тл (от 10 000 до 16 000 Гс) можно вместо предыдущей формулы пользоваться формулой

$\frac{P}{G}={\sigma }_{гист}\cdot B_m^2\cdot \frac{f}{100}.$   (3)

Потери на вихревые токи выражаются формулой

$\frac{P}{G}={\sigma }_{вихр}\cdot B_m^2\cdot {\left(\frac{f}{100}\right)}^2.$   (4)

В последних формулах: P/G — потери в Вт, отнесенные к 1 кг стали, f — частота в Гц, В_m — амплитуда магнитной индукции в Тл.

Значения коэффициентов, зависящие от качества стали и толщины листов, приведены в таблице.

Сорт стали	Толщина листов в мм	α	β	σгист	σвихр	Удельные потери при Вm = 1 Тл в Вт/кг
Обыкновенная динамная сталь	1,0	0,9	3,5	4,4	22,4	7,8
	0,5	0,9	3,5	4,4	5,6	3,6
	0,35	0,9	3,8	4,7	3,2	3,15
Трансформаторная высоколегированная сталь	0,5 Ворота на Газели.	0,4	2,6	3,0	1,2	1,8
	0,35	0,3	2,1	2,4	0,6	1,35

3. Катушка со сталью. В катушке со сталью различают: Ф₀ — основной магнитный поток, линии магнитной индукции которого замыкаются через стальной сердечник, Ф_S — поток рассеяния, линии которого замыкаются через воздух.

Для подсчета э.д.с. рассеяния вводится в расчет индуктивность рассеяния

$L_S=\frac{{\Psi }_S}{I_0}=\frac{w\cdot {\Phi }_S}{I_0},$   (5)

равная отношению потокосцепления потока рассеяния к току холостого хода.

Индуктивное падение напряжения, обусловленное магнитным потоком рассеяния,

${\dot{U}}_S=j{\dot{I}}_0\cdot \omega L_S=j{\dot{I}}_0\cdot x_S.$    (6)

Напряжение, приложенное к катушке со сталью,

$U\approx E^{\prime }=\mathrm{4,44}f\cdot w\cdot {\Phi }_m,$   (7)

где U ≈ U₀ = E' = –E — электродвижущая сила самоиндукции, созданная основным магнитным потоком.

Потери в стали

$P_{ст}=E{I}_0\sin \alpha ,$   (8)

здесь α — угол магнитного запаздывания.

Активная и реактивная составляющие тока катушки соответственно равны

$I_a=I_0\sin \alpha ,I_p=I_{\mu }=I_0\cos \alpha .$   (9)

4. Эквивалентные схемы для реактивной катушки даны на рис. 1 и 2.

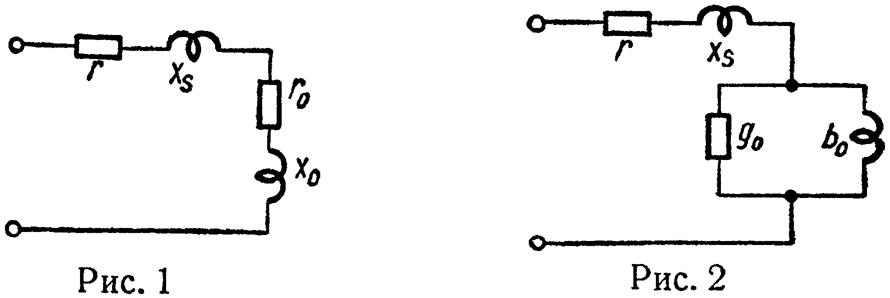
Проводимости g₀ и b₀ в параллельных ветвях схемы рис. 2 определяются из условий

$g_0=\frac{I_a}{E^{\prime }},b_0=\frac{I_{\mu }}{E^{\prime }}.$   (10)

Сопротивления в последовательном варианте схемы рис. 3 определяются из условий

$r_0=\frac{P_{ст}}{I^2},x_0=\sqrt{z_0^2-r_0^2},$   (11)

где

$z_0=\frac{E^{\prime }}{I_0},$

здесь r₀ — активное сопротивление, определяемое потерями в стали, x₀ — индуктивное сопротивление, обусловленное основным магнитным потоком.

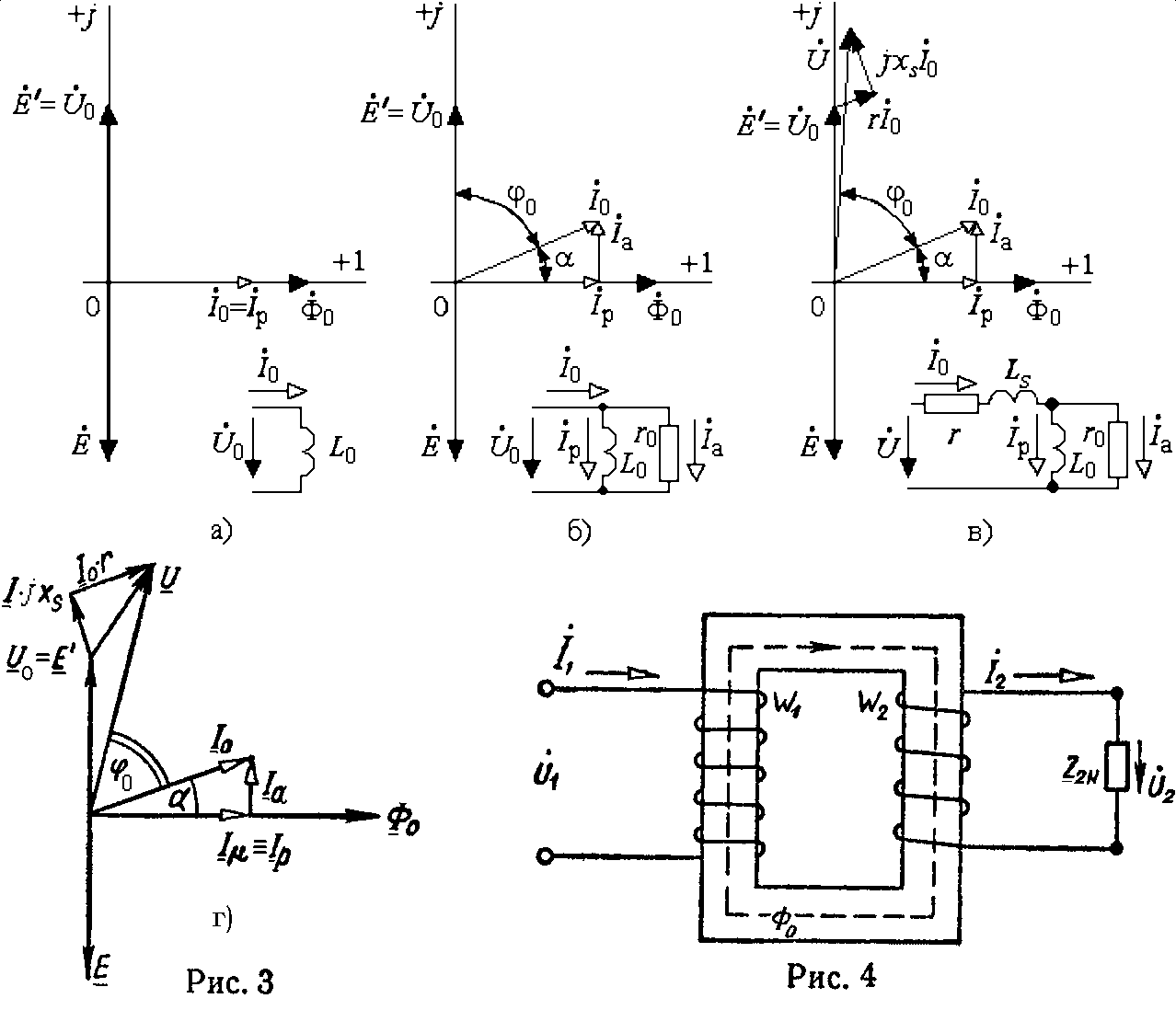
На рис. 3 начерчена векторная диаграмма катушки со стальным сердечником.

5. Трансформатор. Для трансформатора

E₁: E₂ = w₁: w₂ = k,   (12)

где k — коэффициент трансформации, w₁ и w₂ — число витков первичной и вторичной обмоток трансформатора

Магнитный поток трансформатора, работающего при постоянном по амплитуде приложенном напряжении, является практически неизменным при изменении нагрузки и его принимают равным магнитному потоку при холостом ходе трансформатора.

6. Уравнение магнитодвижущих сил трансформатора (рис. 4)

$w_1{\stackrel{?}{I}}_1+w_2{\stackrel{?}{I}}_2=w_1{\stackrel{?}{I}}_0.$   (13)

Основной магнитный поток определяется из соотношения

${\Phi }_0=\frac{w_1{\stackrel{?}{I}}_1+w_2{\stackrel{?}{I}}_2}{R_{м}},$   (14)

где R_м — магнитное сопротивление основному магнитному потоку.

7. Уравнения трансформатора. Токи и э.д.с. в трансформаторе связаны дифференциальными уравнениями

$u_1=i_1{r}_1+L_{1S}\frac{d{i}_1}{dt}+w_1\frac{d{\Phi }_0}{dt}=i_1{r}_1+L_{1S}\frac{d{i}_1}{dt}-e_1,$   (15)

$e_2=-w_2\frac{d{\Phi }_0}{dt}=i_2{r}_2+L_{2S}\frac{d{i}_2}{dt}+u_2,$   (16)

здесь L_1S — индуктивность, обусловленная магнитным потоком рассеяния первой катушки, L_2S — то же, второй катушки, e₁ и e₂ — э.д.с., индуктируемые основным магнитным потоком Ф₀ в первичной и вторичной обмотках

$e_1=w_1\frac{d{\Phi }_0}{dt},e_2=-w_2\frac{d{\Phi }_0}{dt}.$

При синусоидальном напряжении последние уравнения можно записать в символической форме

${\stackrel{?}{U}}_1={\stackrel{?}{I}}_1{r}_1+j\omega L_{1S}{\stackrel{?}{I}}_1+{E^{\prime }}_1,$   (17)

$\{\begin{array}{l}{\stackrel{?}{E}}_2={\stackrel{?}{I}}_2{r}_2+j\omega L_{2S}{\stackrel{?}{I}}_2+{\stackrel{?}{U}}_2,\\ {\stackrel{?}{U}}_2={\stackrel{?}{I}}_2{\underset{\_}{Z}}_2,\end{array}$   (18)

где Z₂ — комплексное сопротивление нагрузки во вторичной цепи.

8. Приведенный трансформатор. Приведенным называется трансформатор, у которого расчетное число витков одной из обмоток принято равным числу витков другой обмотки. Истинные и приведенные сопротивления должны быть в соотношениях (21).

При приведении вторичной обмотки к первичной имеем

${{\stackrel{?}{E}}^{\prime }}_2=-{\stackrel{?}{E}}_{2}k,{{\stackrel{?}{U}}^{\prime }}_2=-{\stackrel{?}{U}}_{2}k,$   (19)

${{\stackrel{?}{I}}^{\prime }}_2=-\frac{{\stackrel{?}{I}}_2}{k},$   (20)

${r^{\prime }}_2=r_2{k}^2,{x^{\prime }}_2=x_2{k}^2,$   (21)

где штрихи относятся к приведенным величинам.

Коэффициент приведения равен коэффициенту трансформации

k = w₁: w₂.

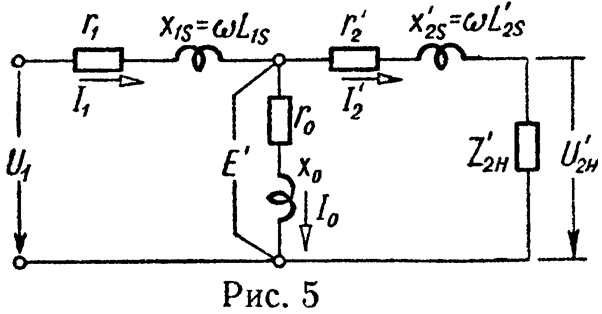
Эквивалентная схема трансформатора изображена на рис. 5.

---

Упражнения и задачи

Задача 1. Известно, что потери в стали при f₁ = 50 Гц Р_1ст = 1,5 Вт/кг, а при f₂ = 100 Гц Р_2ст = 4 Вт/кг.

Разделить потери в стали: на вихревые токи и на магнитный гистерезис, считая, что магнитная индукция остается неизменной.

Решение

Потери в стали на магнитный гистерезис при B_m = const прямо пропорциональны частоте f (формулы 2 и 3), а потери на вихревые токи пропорциональны квадрату частоты (формула 4), поэтому

$\begin{array}{l}{P}_{1ст}=a\cdot f_1+b\cdot f_1^2=a\cdot 50+b\cdot 2500=\mathrm{1,5}\frac{Вт}{кг},\\ P_{2ст}=a\cdot f_2+b\cdot f_2^2=a\cdot 100+b\cdot 10000=4\frac{Вт}{кг},\end{array}$

здесь a и b постоянные коэффициенты, зависящие от сорта стали и величины магнитной индукции.

Решая эти два уравнения, найдем

$a=\mathrm{0,02}\frac{Дж}{кг},b=2\cdot {10}^{-4}\frac{Дж\cdot сек}{кг}.$

Теперь найдем искомые величины

при f₁ = 50 Гц

$$\begin{array}{l}{P}_{1гист}=a\cdot f_1=\mathrm{0,02}\cdot 50=1\frac{Вт}{кг},\\ P_{1вихр}=b\cdot f_1^2=2\cdot {10}^{-4}\cdot 2500=\mathrm{0,5}\frac{Вт}{кг},\end{array}$$

при f₂ = 100 Гц

$$\begin{array}{l}{P}_{2гист}=a\cdot f_2=\mathrm{0,02}\cdot 100=2\frac{Вт}{кг},\\ P_{2вихр}=b\cdot f_2^2=2\cdot {10}^{-4}\cdot 10000=2\frac{Вт}{кг}.\end{array}$$

Задача 2. Катушка со стальным сердечником включена на напряжение U₁ = 100 В и по ней проходит ток I₁ = 5 А, отстающий по фазе от напряжения на угол φ₁, причем cosφ₁ = 0,7. Эта же катушка при том же напряжении, но без стального сердечника потребляет ток I₂ = 10 А, отстающий от напряжения на угол φ₂, причем cosφ₂ = 0,9.

Определить потери в стали и потери в меди и построить векторную диаграмму при наличии стального сердечника.

С помощью векторной диаграммы определить r₀ и x₀ в схеме замещения катушки со стальным сердечником.

Решение

При отсутствии сердечника катушка имеет только потери в меди, равные

$I_2^2\cdot r=U_1{I}_2\cos {\phi }_2.$

Отсюда определяется активное сопротивление обмотки катушки

$r=\frac{U_1\cos {\phi }_2}{I_2}=9Ом.$

При наличии стального сердечника в катушке расходуется мощность

$P_1=U_1{I}_1\cos {\phi }_1=350Вт.$

Часть этой мощности

$P_{м}=I_1^2\cdot r=225Вт$

идет на покрытие потерь в меди и другая часть — на потери в стали

$P_{ст}=P_1-P_{м}=125Вт.$

Эквивалентная схема катушки со сталью, не имеющей рассеяния, дана на рис. 6, а.

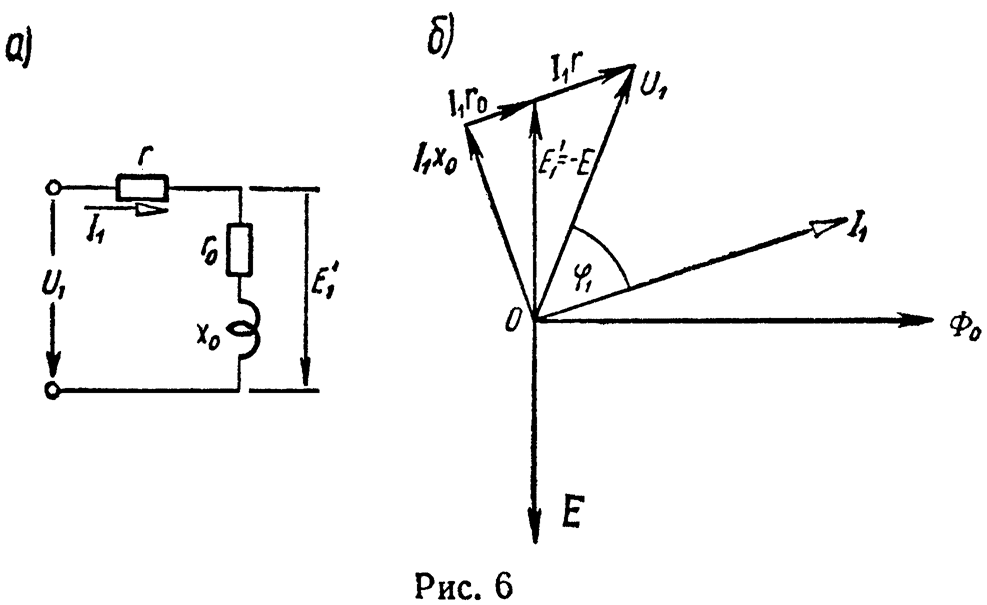
На рис. 6, б начерчена векторная диаграмма катушки со стальным сердечником.

Из векторной диаграммы следует, что активная составляющая приложенного напряжения

$U_1\cos {\phi }_1=I_1\left(r+r_0\right),$

откуда

$r_0=\frac{U_1\cos {\phi }_1}{I_1}-r=\frac{100\cdot \mathrm{0,7}}{5}-9=5Ом.$

Из диаграммы видно, что

$U_1\sin {\phi }_1=I_1{x}_0$

и, следовательно,

$x_0=\frac{U_1\sin {\phi }_1}{I_1}=\frac{100\cdot \mathrm{0,715}}{5}=\mathrm{14,3}Ом.$

Величина э.д.с., наводимой в катушке, будет

$E=I\cdot z=I\cdot \sqrt{r_0^2+x_0^2}=\mathrm{75,6}В.$

Задача 3. Сердечник однофазного трансформатора набран из обыкновенной динамной стали толщиной d = 0,35 мм, имеет прямоугольное сечение 150×100 мм² и длину средней линии магнитной индукции 120 см. Изоляция между листами занимает 10% сечения. Первичная обмотка его состоит из w₁ = 1500 витков и включена на напряжение U₁ = 6000 В. Определить потери в стали. Частота переменного тока f = 50 Гц.

Указание. Воспользовавшись формулой (7), определить магнитный поток Ф_m. Зная активное сечение сердечника S = 0,9×15·10·10^–4 м², найти магнитную индукцию B_m. Потери в стали найдутся по формулам (3) и (4).

Ответ: P_ст = 710 Вт.

Задача 4. Однофазный трансформатор имеет первичное напряжение U₁ = 3300 В и вторичное U₂ = 220 В. Сердечник его имеет сечение S = 100 см² и вес G = 350 кг и набран из листов электротехнической стали Э11 толщиной d = 0,35 мм. Максимальная магнитная индукция в сердечнике B_m = 0,8 Тл (8000 Гс). Определить необходимое число витков первичной и вторичной обмоток, ток холостого хода и коэффициент мощности трансформатора при холостом ходе. Частота переменного тока f = 50 Гц.

Решение

Из формулы (7) найдем, что

$w_1=\frac{U_1}{\mathrm{4,44}{\Phi }_{m}f}=1860иw_1=w_1\cdot \frac{U_2}{U_1}=124.$

Средняя длина магнитопровода, равная длине средней линии магнитной индукции, найдется из формулы: G = S·l·d, где плотность стали d = 7,6 г/см³.

Отсюда l = 4,6 м.

По кривой намагничивания для листовой стали найдем, что при B_m = 0,8 Тл Н_m = 318 А/м.

Магнитодвижущая сила (амплитудное значение) будет равна

F_m = H_m·l = 318·4,6= 1460 А,

и так как

F_m = w·I_mμ = 1460 А,

то ток намагничивания

$I_{\mu }=\frac{F}{\sqrt{2}\cdot w_1}=\frac{1460}{\sqrt{2}\cdot 1860}=\mathrm{0,555}А.$

Потери в стали определяем по формулам (2) и (4)

$\begin{array}{l}P=\left[\alpha \cdot B_m\cdot \frac{f}{100}+\beta \cdot B_m^2\cdot \frac{f}{100}+{\sigma }_{вихр}\cdot B_m^2\cdot {\left(\frac{f}{100}\right)}^2\right]\cdot G=\\ =\left[\mathrm{0,9}\cdot \mathrm{0,8}\cdot \mathrm{0,5}+\mathrm{3,8}\cdot \mathrm{0,64}\cdot \mathrm{0,5}+\mathrm{3,2}\cdot \mathrm{0,64}\cdot \mathrm{0,25}\right]\cdot 350=\\ =\mathrm{2,09}\cdot 350=730Вт.\end{array}$

Так как

$P_{ст}=U_1{I}_a,$

то

$I_a=\frac{P_{ст}}{U_1}=\frac{730}{3300}=\mathrm{0,22}А.$

Ток холостого хода

$\begin{array}{l}{I}_0=\sqrt{I_{\mu }^2+I_a^2}=\mathrm{0,595}А\\ cos{\phi }_0=\frac{I_a}{I_0}=\mathrm{0,37.}\end{array}$

На рис. 7 приведена векторная диаграмма холостого хода трансформатора.

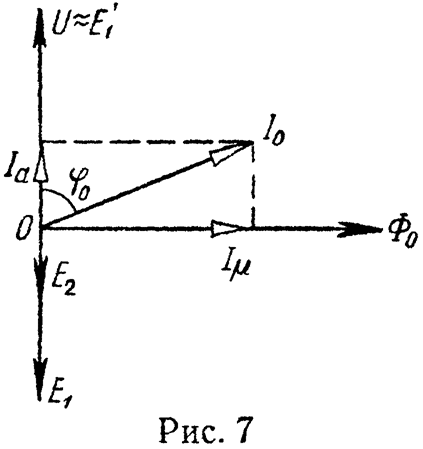
Задача 5. В катушке со стальным сердечником расходуется мощность P = 0,2 кВт при напряжении U = 100 В и токе I = 10 А. Активное сопротивление обмотки r = 0,5 Ом и реактивное сопротивление рассеяния x_S = 1 Ом. Частота тока f =50 Гц.

Определить из векторной диаграммы намагничивающий ток I_μ, сопротивления r₀ и x₀, и составляющую приложенного напряжения E', преодолевающую э.д.с., которая индуктируется в обмотке катушки основным магнитным потоком, пронизывающим сердечник.

При построении диаграммы предполагать, что ток изменяется по гармоническому закону.

Решение

На рис. 1 дана эквивалентная схема катушки со сталью имеющей рассеяние, и на рис. 8 — ее векторная диаграмма.

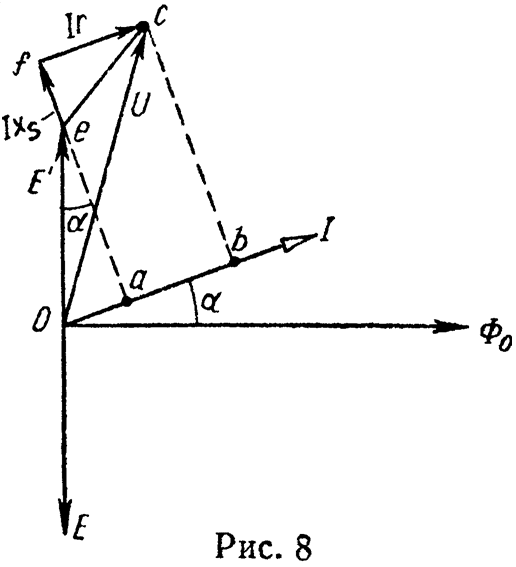
Из соотношения P = UIcosφ найдем, что cosφ = 0,2.

Отрезок

$Ob=I\left(r+r_0\right)=U\cos \phi ,$

отсюда

$r_0=\frac{U\cos \phi }{I}-r=\mathrm{1,5}Ом.$

Отрезок

$bc=U\sin \phi =\mathrm{97,9,}$

с другой стороны, bc = ae + ef = Ix₀ + Ix_S, отсюда

x₀ = 8,79 Ом.

Теперь найдем

$E^{\prime }=\sqrt{O{a}^2+a{e}^2}=I\sqrt{r_0^2+x_0^2}=\mathrm{88,5}В.$

Намагничивающий ток

$I_{\mu }=I\cos \alpha =10\cdot \frac{\mathrm{87,9}}{\mathrm{88,5}}=\mathrm{9,94}А.$

Задача 6. По заданным на рис. 9, а петле магнитного гистерезиса и синусоидальной кривой магнитного потока построить кривую изменений тока во времени в обмотке катушки со сталью и определить потери мощности на гистерезис.

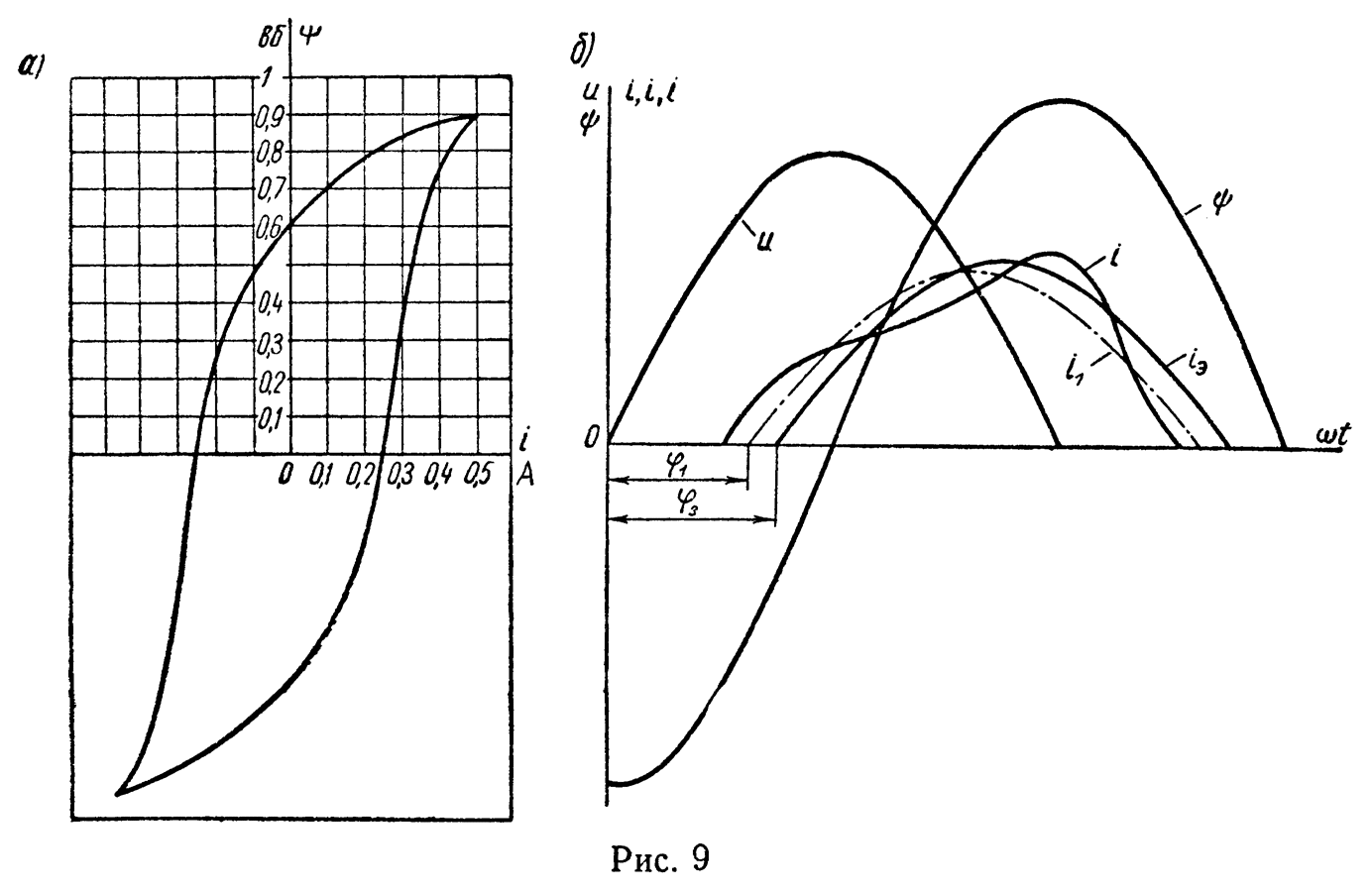
Частота f = 50 Гц. Активным сопротивлением обмотки пренебречь. На рис. 9, а буквой ψ обозначено полное число сцеплений потока со всеми витками обмотки (полное потокосцепление обмотки).

Указание. На рис. 9, б по заданной петле магнитного гистерезиса и кривой магнитного потокосцепления ψ построена кривая тока i.

Полученная кривая тока i должна быть разложена в гармонический ряд одним из графических способов. При этом будут найдены амплитуды и фазы гармонических составляющих относительно выбранного начала разложения. На основе результатов графического разложения на рис. 9, б нанесены первая гармоника тока i₁ и эквивалентная синусоида тока i_Э.

Действующее значение эквивалентного тока найдется по формуле

$I_{Э}=\sqrt{I_1^2+I_3^2+I_5^2}.$

Действующее значение приложенного напряжения определится по формуле (7).

Расходуемая мощность может быть определена по формуле

P = UI₁cosφ₁,

где I₁ — ток основной гармоники, φ₁ — его фаза были определены выше из графического разложения. Других слагаемых формула мощности не имеет, так как приложенное напряжение синусоидально.

Эта мощность, очевидно, и равна потерям на магнитный гистерезис.

Наконец, можно найти фазу эквивалентного тока из соотношения

UI₁cosφ₁ = UI_Эcosφ_Э.

Отсюда видно, что так как I_Э > I₁, то cosφ_Э < cosφ₁ и φ_Э > φ₁.

Ответ: P = 35,4 Вт; на основе разложения кривой в ряд имеем: I_1m = 0,46 А, I_3m = 0,1 А, I_5m = 0,02 А, φ₁ = 57°, φ_Э = 57,83°.

Задача 7. Однофазный трансформатор с коэффициентом трансформации k = w₁: w₂ = 2 с разомкнутой вторичной обмоткой приключен к сети с напряжением U = 220 В. Полагая, что трансформатор изготовлен из обыкновенной динамной стали (удельный вес 7,8 г/см³), толщина листов которого d = 0,5 мм, определить потери в стали, величину тока в обмотке и построить векторную диаграмму. Потоком рассеяния пренебречь.

Число витков первичной обмотки w₁ = 74, активное сечение сердечника S = 100 см², средняя длина сердечника l_ср = 150 см. Частота f =50 Гц.

Указание. При определении магнитной индукции в стали трансформатора в первом приближении можно считать напряжение на зажимах равным э.д.с. обмотки трансформатора. Для определения намагничивающей составляющей тока необходимо при расчете магнитной цепи воспользоваться кривой намагничивания для листовой стали Э11.
Ответ: P_ст = 757 Вт, I₀ = 26,6 А.

Задача 8. Однофазный трансформатор U₁/U₂ = 6600/220 в с номинальной мощностью S = 50 кВА имеет потери холостого хода P_х = 380 Вт и к.п.д. при полной нагрузке η = 96,15% с cosφ₂ = 0,8.

Определить активное сопротивление первичной и вторичной обмоток, считая, что первичные и вторичные потери в меди одинаковы.

Решение

Известно, что ток холостого хода имеет незначительную величину по сравнению с номинальным током. Поэтому при холостом ходе можно пренебречь потерями в обмотке (потерями в меди) и считать, что потери холостого хода приблизительно равны потерям в стали;

P_х = P_ст = 380 Вт.

Общие потери мощности при нагрузке трансформатора равны

$P_{м}+P_{ст}=\frac{\left(1-\eta \right)S\cos {\phi }_2}{100}=1540Вт.$

Отсюда

$\begin{array}{l}{P}_{м}=1540-380=1160Вт,\\ P_{1м}=P_{2м}=\frac{1160}{2}=580Вт.\end{array}$

Номинальный ток в первичной цепи при нагрузке

$I_1=\frac{P}{U_1}=\mathrm{7,6}А,$

активное сопротивление первичной обмотки

$r_1=\frac{P_{1\mu }}{I_1^2}=\mathrm{10,1}Ом.$

Так как по условию активное сопротивление первичной обмотки равно приведенному сопротивлению вторичной

$r_1={r^{\prime }}_2=r_2\cdot k^2,$

где

$k=\frac{6600}{220}=\mathrm{30,}$

то

$r_2=\frac{\mathrm{10,1}}{{30}^2}=\mathrm{0,011}Ом.$

Задача 9. Опыты холостого хода и короткого замыкания однофазного трансформатора дали следующие результаты: холостой ход – U_1х = 400 В, I_1х = 0,4 А, Р_1х = 20 Вт, короткое замыкание — U_1к = 32 В, I_1к = 5 А, Р_1к = 80 Вт.

Данный трансформатор повышающий и имеет коэффициент трансформаций

k = w₁: w₂ = 1: 15.

Предполагая активное и реактивное сопротивление рассеяния первичной обмотки равными соответственным приведенным сопротивлениям вторичной обмотки (r₁ = r'₂ = r и x_1S = x_2S = x₂), определить их величины.

При холостом ходе можно пренебречь падением напряжения в первичной обмотке. При коротком замыкании можно пренебречь намагничивающей составляющей первичного тока.

Решение

На рис. 5 изображена эквивалентная схема трансформатора.

Из опыта холостого хода, пренебрегая падением напряжения в первичной обмотке, имеем

$\begin{array}{l}{z}_x=\frac{U_{1x}}{I_{1x}}=1000Ом,\\ cos{\phi }_x=\frac{P_{1x}}{U_{1x}\cdot I_{1x}}=\mathrm{0,125,}\\ r_x=z_x\cos {\phi }_x=125Ом,\\ x_x=z_x\sin {\phi }_x=992Ом.\end{array}$

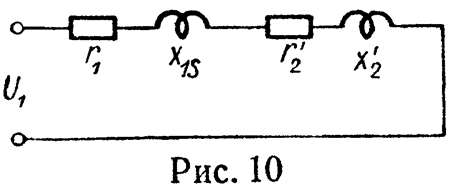
Пренебрегая намагничивающей составляющей тока, эквивалентная схема трансформатора при коротком замыкании примет вид, изображенный на рис. 10, и тогда

$\begin{array}{l}{z}_{к}=\frac{U_{1к}}{I_{1к}}=\mathrm{6,4}Ом,cos{\phi }_{1к}=\frac{P_{1к}}{U_{1к}\cdot I_{1к}}=\mathrm{0,5,}\\ r_1+{r^{\prime }}_2=z_{к}cos{\phi }_{1к}=\mathrm{3,2}Ом,x_{1S}+{x^{\prime }}_{2S}=z_{к}\sin {\phi }_{1к}=\mathrm{5,54}Ом.\end{array}$

Так как

$r_1={r^{\prime }}_2,x_{1S}={x^{\prime }}_{2S},$

то

$\begin{array}{l}{r}_1=\mathrm{1,6}Ом,r_2=\frac{{r^{\prime }}_2}{k^2}=360Ом,\\ x_{1S}=\mathrm{2,77}Ом,x_{2S}=\frac{{x^{\prime }}_{2S}}{k^2}=623Ом.\end{array}$

Задача 10. Ко вторичным зажимам трансформатора предыдущей задачи приключен приемник энергии, имеющий cosφ₂ = 0,92 (φ₂ > 0), при этом напряжение на вторичных зажимах U₂ = 6000 В, сила тока во вторичной цепи I₂ = 0,25 А.

Найти напряжение на первичных зажимах — U₁, силу тока в первичной обмотке — I₁, коэффициент полезного действия — η и коэффициент мощности — cosφ₁.

Найти потери в стали и меди при нагрузке трансформатора.

Замечание. Из предыдущей задачи, пренебрегая падением напряжения в первичной обмотке, имеем

$\begin{array}{l}{r}_0\approx r_x=125Ом,x_0\approx x_x=992Ом,\\ {\underset{\_}{z}}_0=r_0+j{x}_0=125+j992=1000e^{j\mathrm{82,82}°}Ом.\end{array}$

Решение

Задачу проще всего решить, если применить символический метод к эквивалентной схеме трансформатора (рис. 5).

Приведенные величины вторичного напряжения, тока и сопротивлений будут

$\begin{array}{l}{U^{\prime }}_2=U_2\cdot k=400В,\\ {I^{\prime }}_2=\frac{I_2}{k}=\mathrm{3,75}А,\\ {z^{\prime }}_{2н}=\frac{U_2}{{I^{\prime }}_2}=\mathrm{106,6}Ом,\\ {r^{\prime }}_{2н}={z^{\prime }}_{2н}\cos {\phi }_2=98Ом,\\ {x^{\prime }}_{2н}={z^{\prime }}_{2н}\sin {\phi }_2=\mathrm{41,6}Ом.\end{array}$

Напряжение E' на параллельных ветвях будет

${\stackrel{?}{E}}^{\prime }={{\stackrel{?}{I}}^{\prime }}_2\cdot \left[\left({r^{\prime }}_{2н}+{r^{\prime }}_2\right)+\left({x^{\prime }}_{2н}+{x^{\prime }}_{2S}\right)\right]=\mathrm{373,8}+j\mathrm{166,5}=409e^{j\mathrm{24,01}°}В,$

где I'₂ направлен по действительной оси и, следовательно,

$\begin{array}{l}{{\stackrel{?}{I}}^{\prime }}_2={I^{\prime }}_2=\mathrm{3,75}А,\\ {\stackrel{?}{I}}_0=\frac{{\stackrel{?}{E}}^{\prime }}{{\underset{\_}{z}}_0}=\mathrm{0,41}{e}^{-j\mathrm{58,82}°}=\mathrm{0,21}-j\mathrm{0,35}А,\\ {\stackrel{?}{I}}_1={{\stackrel{?}{I}}^{\prime }}_2+{\stackrel{?}{I}}_0=\mathrm{3,96}-j\mathrm{0,35}=\mathrm{3,97}{e}^{-j\mathrm{5,05}°}.\end{array}$

Приложенное напряжение

${\stackrel{?}{U}}_1={\stackrel{?}{I}}_1{\underset{\_}{z}}_1+{\stackrel{?}{E}}^{\prime }=\mathrm{383,5}+j\mathrm{174,6}=421e^{j\mathrm{24,48}°}В.$

Сдвиг фаз между напряжением на входе трансформатора и первичным током

${\phi }_1=\mathrm{24,48}°-\left(-\mathrm{5,05}°\right)=\mathrm{29,53}°.$

Мощность, подводимая к трансформатору,

$P_1=U_1{I}_1\cos {\phi }_1=1450Вт.$

Мощность, расходуемая в приемнике энергии,

$P_2=U_2{I}_2\cos {\phi }_2=1380Вт.$

Коэффициент полезного действия трансформатора

$\eta =\frac{P_2}{P_1}=\mathrm{0,95.}$

Потери в стали при нагрузке трансформатора

$P_{ст}=I_0^2{r}_0=21Вт.$

Потери в меди при нагрузке трансформатора

$P_{м}=P_1-P_2-P_{ст}=49Вт.$

Задача 11. К трансформатору задачи 9 приложено напряжение U₁ = 420 В.

Найти величину напряжения E₂ на вторичных зажимах при холостом ходе, пренебрегая при этом падением напряжения в первичной обмотке. Показать возможность такого пренебрежения.

Решение

При холостом ходе можно положить U₁ ≈ E₁ = 420 В. Тогда

$$E_2=\frac{E_1}{k}=6300В.$$

Пренебречь падением напряжения в первичной обмотке можно, так как

$\frac{I_0{z}_1}{E_1}\cdot 100\%=\frac{\mathrm{0,41}\cdot \mathrm{3,2}}{420}=\mathrm{0,3}\%,$

т.е. падение напряжения в первичной обмотке составляет всего 0,3% от приложенного напряжения.

---

Скачать статью Катушки и трансформаторы со стальными сердечниками

---

Катушка со стальным сердечником подключена к источнику синусоидального напряжения. При напряжении источника U = 100 В ток в катушке I = 0,1 А, а потребляемая мощность P = 1,58 Вт. Активное сопротивление провода обмотки R_К = 6 Ом, индуктивное сопротивление, обусловленное потоком рассеяния, X_S = 3 Ом.

Определить:

1. Мощность потерь в стали сердечника.

2. Намагничивающий I_P и обусловленный потерями в стали I_а токи.
Скачать решение задачи Катушка со стальным сердечником подключена к источнику

---

Катушка с числом витков w = 500 и магнитопроводом из трансформаторной стали включена в сеть с напряжением U = 220 В (частота 50 Гц). Ток катушки I = 10 А, активная мощность Р = 1500 Вт. Сопротивление обмотки из медного провода постоянному току R_м = 10 Ом. Амплитуда потока в магнитопроводе Ф_m =10^–3 Вб.

Составить параллельную схему замещения катушки и построить векторную диаграмму.
Скачать решение задачи Параллельная схема замещения катушки со сталью и векторная диаграмма

---

Магнитопровод катушки имеет сечение S = 6 см², массу М = 1,4 кг. Число витков обмотки w = 1200. Активное сопротивление обмотки R_м = 30 Ом, индуктивное сопротивление рассеяния X_S = 60 Ом. Напряжение питания U = 220 В, частота 50 Гц.

Определить ток в катушке. Известна зависимость удельных потерь P₀ (B_m) и удельной мощности намагничивания Q₀ (B_m).
Скачать решение задачи Определение тока в катушке по известной зависимости удельных потерь и удельной мощности намагничивания

---

Типовой расчет НИУ МЭИ

РАСЧЕТ УСТАНОВИВШИХСЯ РЕЖИМОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ ПЕРЕМЕННОГО ТОКА

Часть II Катушка со стальным сердечником в цепи переменного тока

Скачать решение Катушка со стальным сердечником в цепи переменного тока

катушка со сталью, потери в стали, потери в меди, основной магнитный поток, магнитный поток рассеяния, Трансформаторы, коэффициент трансформации, уравнения трансформатора, приведенный трансформатор, эквивалентная схема трансформатора, коэффициент мощности трансформатора