2.3 Магнитное поле, индуктивность
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 2 Магнитное поле и магнитные цепи при постоянных токахМагнитное поле, индуктивность
Основные положения и соотношения
1. Закон Био — Савара — Лапласа выражает значение магнитной индукции, определяемой элементом тока на расстоянии r от него в однородной среде (рис. 1)
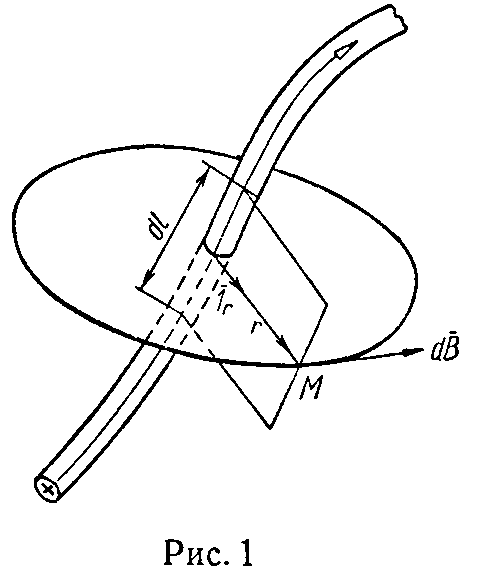
(1)
здесь
– единичный вектор, направленный от центра элемента тока в точку М, в которой определяется магнитная индукция;
r — расстояние от центра элемента тока до той же точки;
µ — абсолютная магнитная проницаемость среды, равная µ0·µr;
µr — магнитная проницаемость (относительная магнитная проницаемость);
– магнитная постоянная.
В формуле (1) использовали векторное произведение
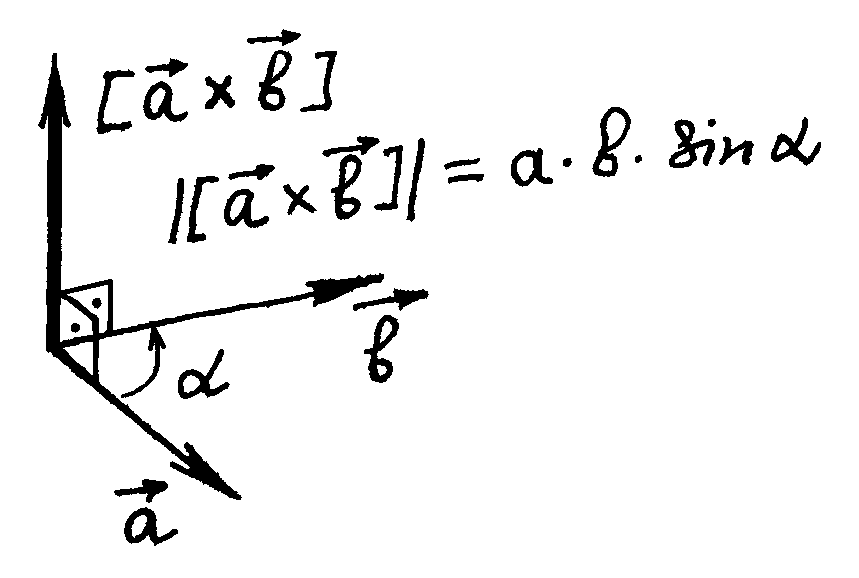
Закон Био — Савара — Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био — Савара — Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
Связь между векторами напряженности магнитного поля и магнитной индукцией выражается формулой
(2)
Величина напряженности магнитного поля тока, протекающего по прямому проводнику конечной длины l (рис. 2) в некоторой точке, находящейся на расстоянии a от проводника, равна
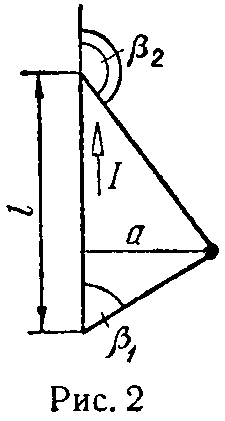
(3)
Направление вектора определяется правилом винта; так, в рассматриваемой на рис. 2 точке вектор направлен от читателя за чертеж.
Величина напряженности магнитного поля прямого и бесконечно длинного тока в точке, отстоящей на расстоянии a от оси провода, несущего ток, равна
(4)
Величина напряженности магнитного поля кругового тока в некоторой точке на его оси (рис. 3) определяется по формуле
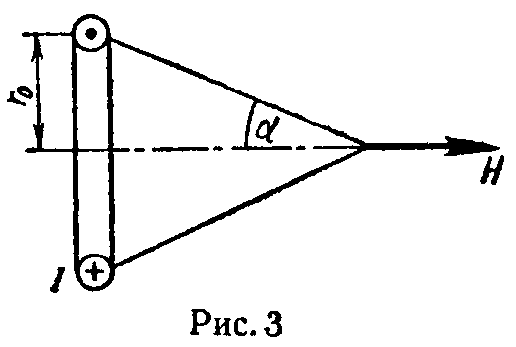
(5)
здесь r0 — радиус витка, по которому протекает круговой ток, α — угол, под которым виден радиус витка из точки, в которой определяется напряженность поля.
Напряженность магнитного поля в центре плоскости витка определяется по формуле
(6)
Напряженность магнитного поля соленоида. Величина напряженности магнитного поля в некоторой точке на оси цилиндрического соленоида (рис. 4)
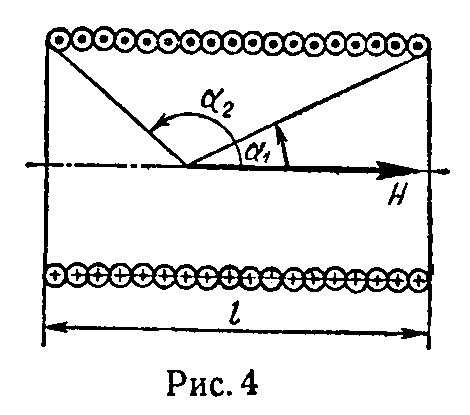
(7)
здесь w — общее число витков соленоида.
Величина напряженности магнитного поля на оси очень длинного цилиндрического соленоида
(8)
Направление вектора и здесь определяется правилом винта.
По этой же формуле находится напряженность магнитного поля на оси кольцевого соленоида (тороида). В этом случае l — длина средней линии магнитной индукции, считается совпадающей с кольцевой осью соленоида.
2. Закон полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
(9)
Формулы (4) и (8) являются непосредственными результатами применения закона полного тока.
3. Поток вектора магнитной индукции сквозь поверхность S
(10)
4. Сила Лоренца. Сила, испытываемая зарядом q, движущимся со скоростью v в магнитном поле с индукцией В, определяется по формуле
(11)
Макроскопическим проявлением силы Лоренца является сила Ампера.
Закон Ампера. Сила (рис. 5), действующая на элемент провода с током I , помещенный в магнитное поле с индукцией (сила Ампера),
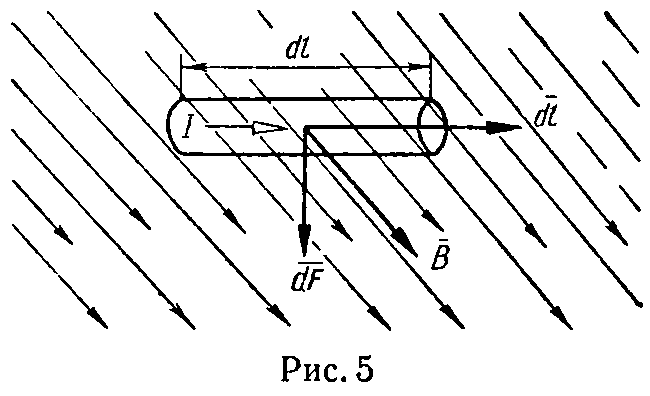
(12)
Прямолинейный проводник длиной l, помещенный в однородное магнитное поле с индукцией под углом α к вектору , испытывает силу
(13)
где – единичный вектор, нормальный к плоскости, проведенной через векторы и .
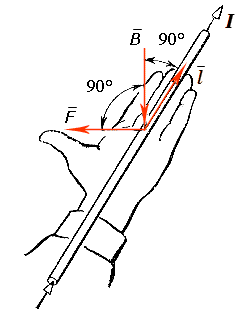
Направление силы Ампера F определяется правилом левой руки.
5. Работа сил поля при перемещении в нем на расстояние ds элемента проводника длиною dl с током I равна (рис. 6)
(14)
здесь dФ — магнитный поток через поверхность, описанную проводником при его перемещении.
Работа, производимая при перемещении замкнутого контура с неизменным по величине током в постоянном магнитном поле, определяется выражением
(15)
где Ф1 и Ф2 — величины магнитного потока, пронизывающего контур в начальном и конечном положениях.
6. Расчет магнитных цепей. Основанием к расчету служат: первый закон Кирхгофа для магнитных цепей и закон полного тока.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к контуру, образованному средними магнитными линиями магнитной цепи и имеет вид
(16)
Величина F называется магнитодвижущей силой (МДС).
Выражение
(17)
называют вторым законом Кирхгофа для магнитных цепей и формулируют следующим образом: алгебраическая сумма магнитодвижущих сил (ΣwI) в замкнутом контуре магнитной цепи равна алгебраической сумме магнитных напряжений в том же контуре.
В формуле (17) – магнитное сопротивление участка цепи с сечением Sk, с длиною средней магнитной линии lk и с абсолютной магнитной проницаемостью материала µk.
Отметим, что для расчета стальной магнитной цепи формулой (17) пользуются редко, так как Rмk не может рассматриваться как постоянная величина (величина магнитной проницаемости стали и других ферромагнитных материалов зависит от их намагниченности).
При расчете магнитодвижущей силы для воздушного зазора напряженность магнитного поля определяется по формуле
(18)
7. Закон электромагнитной индукции. Величина индуктированной ЭДС
(19)
где Ψ — потокосцепление. Оно может быть выражено произведением величины магнитного потока на число витков, с которыми он сцеплен
(20)
8. Общее выражение для статической индуктивности проводника, витка, катушки
(21)
9. ЭДС, индуктированная в прямолинейном проводнике, движущемся с равномерной скоростью v в однородном магнитном поле, равна
e = B·l·v·sinα, (22)
где α — угол между направлениями векторов и .
10. Величина ЭДС самоиндукции
(23)
11. Индуктивность соленоида
(24)
здесь w — число витков, S — сечение соленоида, l — длина средней линии магнитной индукции.
Эта же формула приближенно подходит для расчета индуктивности длинной однослойной катушки цилиндрической формы (l/D > 50), где l/D –отношение длины катушки к диаметру ее витков.
12. Для вычисления индуктивности коротких цилиндрических катушек без стального сердечника применяется формула
(25).
где коэффициент k является функцией отношения диаметра D катушки к ее длине l его значения приведены в таблице 1.
Таблица 1 — Значения коэффициент k(D/l)
|
D/l |
k |
D/l |
k |
|
0,00 |
1,0000 |
1,00 |
0,6884 |
|
0,10 |
0,9588 |
0,80 |
0.6581 |
|
0,20 |
0,9201 |
0,60 |
0.5697 |
|
0,40 |
0,8499 |
0,40 |
0,4719 |
|
0,60 |
0,7885 |
0,20 |
0,3108 |
|
0,80 |
0,7351 |
0,10 |
0,2033 |
|
1,00 |
0,6884 |
|
|
13. Индуктивность двухпроводной линии
(26)
здесь D — расстояние между осями проводов, r — радиус провода, l — длина линии, µ — абсолютная магнитная проницаемость проводов линии.
Для проводников, изготовленных не из ферромагнитных материалов, пользуются следующей приближенной формулой, в которой отсутствует слагаемое, выражающее внутреннюю индуктивность
(27)
Индуктивность однопроводной линии
(28)
где h — высота провода над землей.
14. Общее выражение для взаимной индуктивности двух контуров
(29)
здесь w1 и I1 — число витков и ток, проходящий в первом контуре, Ф21 — часть общего магнитного потока, определяемого током второго контура и пронизывающего первый контур, w2 и I2 — число витков и ток, проходящий во втором контуре, Ф12 — часть общего магнитного потока, определяемого током первого контура и пронизывающего второй контур.
15. Электродвижущая сила взаимоиндукции двух контуров с токами
(30)
здесь e1M — ЭДС, наведенная в первом контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф21, определяемого током во втором контуре, со скоростью , e2M — ЭДС, наведенная во втором контуре вследствие изменения во времени сцепляющейся с ним части магнитного потока Ф12, определяемой током в первом контуре, со скоростью .
16. Взаимная индуктивность двух кольцевых соленоидов, имеющих общий сердечник, число витков которых w1 и w2, определяется по приближенной формуле
(31)
здесь S — сечение сердечника, l — длина средней линии магнитной индукции.
Взаимная индуктивность между двумя параллельными двухпроводными линиями a1a2 и b1b2 длиною l (рис. 7)
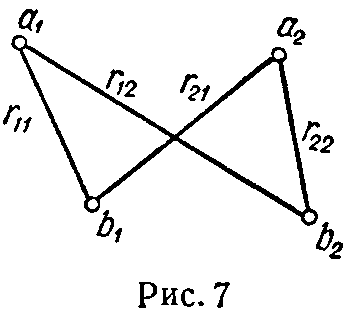
(32)
Расстояния считаются между осями проводов. Радиусы проводов предположены малыми по сравнению с расстояниями между ними.
17. Заряд, прошедший через проводящий контур. Количество индуктированного электричества, прошедшего через проводящий контур, имеющий w витков, при изменении сцепленного с ним магнитного потока от величины Ф1 до величины Ф2
(33)
здесь r — сопротивление контура, w — число витков.
18. Коэффициент магнитной связи двух контуров
(34)
Пределы изменения коэффициента магнитной связи
0 ≤ k ≤ 1.
Коэффициент рассеяния
σ = 1 — k2. (35)
19. Энергия магнитного поля
(36)
где Ψ — потокосцепление.
Удельная энергия магнитного поля (на единицу объема)
(37)
Энергия магнитного поля может быть выражена через удельную энергию посредством интеграла
(38)
здесь V — объем пространства, занятый магнитным полем.
20. Полная магнитная энергия системы двух индуктивно связанных контуров с токами I1 и I2
(39)
Упражнения и задачи
Задача 1. Вычислить и построить кривую, зависимости напряженности магнитного поля неограниченно длинного коаксиального кабеля (рис. 8) в функции расстояния r от его оси, если по кабелю проходит постоянный ток I = 1 А.
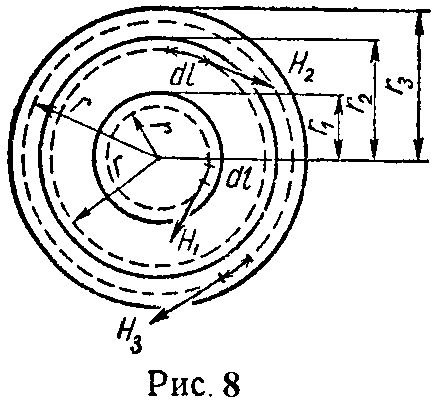
Радиус внутреннего проводника r1 = 2 мм, радиусы трубы r2 = 7,2 мм и r3 = 7,5 мм.
Плотность тока по сечению каждого проводника распределена равномерно.
Решение
Для определения напряженности магнитного поля (ввиду симметрии) воспользуемся законом полного тока.
Область внутреннего проводника (0 ≤ r ≤ r1)
Проведем окружность радиуса r < r1 с центром на оси провода. В любой ее точке напряженность H1 вследствие симметрии имеет одно и то же значение и совпадает по направлению с элементом длины окружности . Беря линейный интеграл напряженности магнитного поля вдоль этой окружности, по закону полного тока получим
где под I(r) надо понимать ток, проходящий в части сечения проводника, находящейся внутри контура циркуляции.
Плотность тока во внутреннем проводнике
Ток, проходящий через часть сечения проводника, имеющую радиус r < r1,
Итак,
отсюда
После подстановки числовых значений получим
Область полости трубы (r1 ≤ r ≤ r2)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
отсюда
Область трубы (r2 ≤ r ≤ r3)
Применим закон полного тока к окружности радиуса r, проведенной в сечении трубы
Здесь под ΣI надо понимать сумму токов, находящихся внутри окружности радиуса r, т. е. весь ток I, проходящий по внутреннему проводу, и ток, проходящий по части сечения кольца трубы, обходимой контуром циркуляции, причем этот последний ток должен быть взят со знаком минус (так как по трубе протекает обратный ток).
Плотность тока в трубе
Итак,
отсюда
Область пространства вне кабеля (r3 ≤ r)
Для всех точек пространства вне кабеля напряженность магнитного поля H4 = 0. Это вытекает из закона полного тока при любом контуре интегрирования, охватывающем весь кабель.
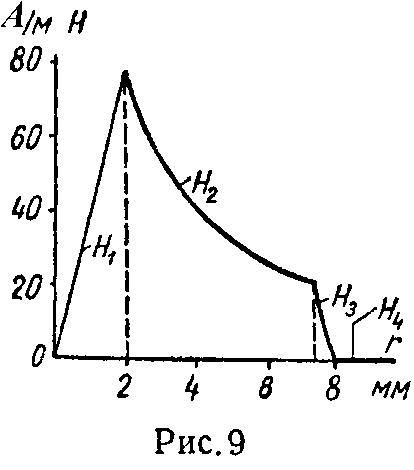
На рис. 9 представлена кривая изменения напряженности магнитного поля в функции r.
Задача 2. Вдоль длинного трубчатого провода, радиусы сечения которого r1 и r2, протекает постоянный ток I (рис. 10).
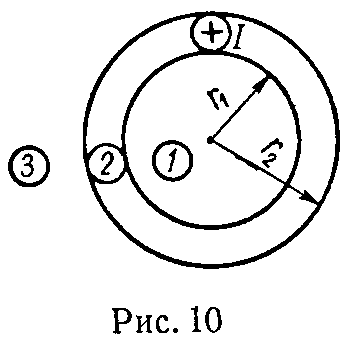
Вычислить и построить кривую зависимости напряженности магнитного поля в функции r — расстояния от точки до оси провода для областей 1 (внутри трубы), 2 (в стенках трубы), 3 (вне трубы). Даны: r1 = 2 см; r2 = 3 см, I = 10 А.
Ответ: внутри трубы (0 ≤ r ≤ r1) H1 = 0; в стенках трубы (r1 ≤ r ≤ r2) ; вне трубы (r2 ≤ r)
Задача 3. Построить кривую напряженности магнитного поля вдоль оси x для двухпроводной линии (рис. 11), оси проводов которой отстоят друг от друга на расстоянии D = 30 см.
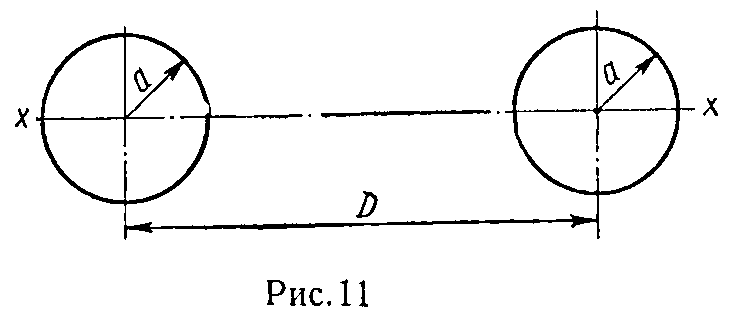
Радиус проводов a = 4 мм. Ток в прямом и обратном проводе I = 200 А. Весь ток, протекающий в проводе, следует считать сосредоточенным в его оси.
Задача 4. Два провода линии электропередачи Л1 и Л2 и две пары телефонных проводов (a1a2 и b1b2 расположены параллельно друг другу (рис. 12, а).
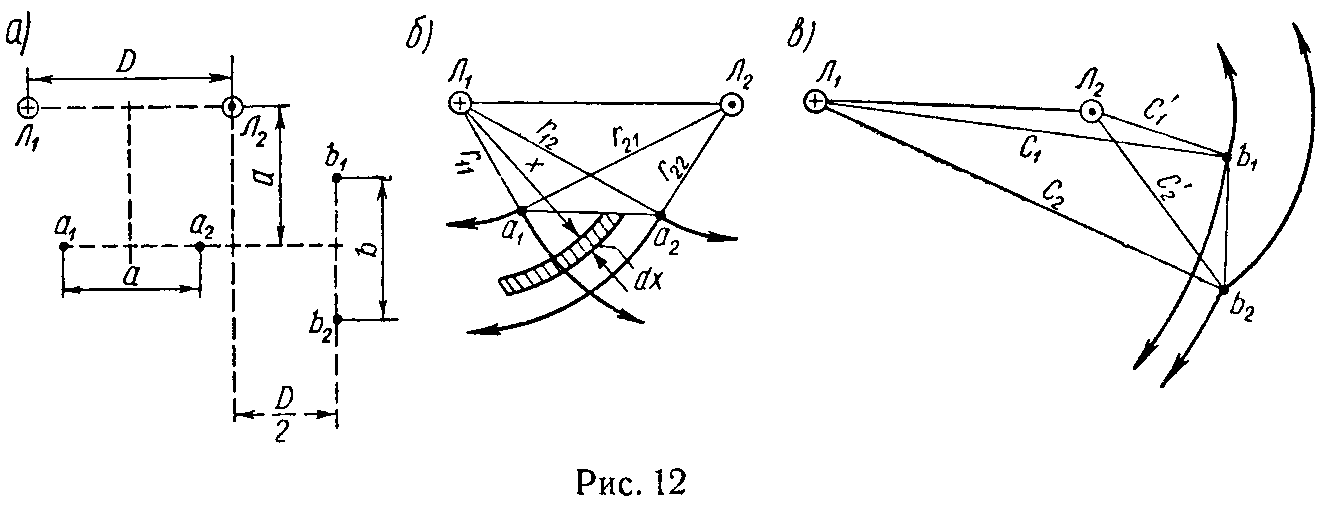
Если по проводам линии передачи проходит ток I = 150 А, то чему будет равно потокосцепление на 1 км с телефонной линией a1a2 и с телефонной линией b1b2. Даны: D = 90 см; a = b = 30 см.
Решение
Найдем потокосцепление линии Л1Л2 с линией a1a2 (рис. 12, б). Поток, определяемый током, проходящим через провод Л1, и пронизывающий линию a1a2, с учетом формул (2), (4) и того, что dS = ldx, где l — длина линии, будет равен
Поток, определяемый током, проходящим через провод Л2, будет равен
Так как
то общий поток
Аналогично найдем, что потокосцепление линии Л1Л2 с линией b1b2 (рис. 12, в) будет равно
Задача 5. На кольцевой эбонитовый сердечник намотано w = 800 витков, по которым проходит ток I = 10 А (рис. 13).
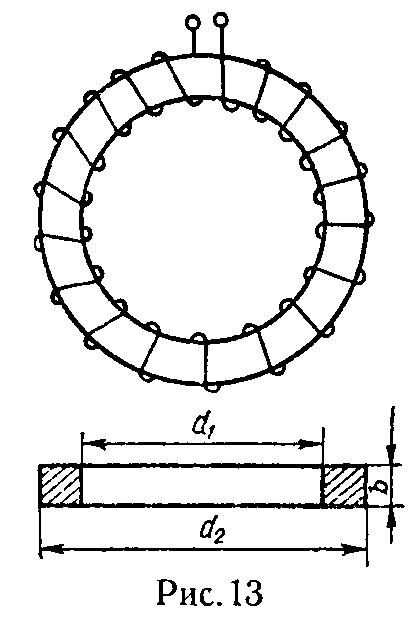
Учитывая неравномерность индукции по сечению сердечника, вычислить значение магнитного потока, проходящего через сердечник.
Внутренний диаметр сердечника d1 = 20 см, внешний диаметр d2 = 25 см, толщина сердечника b = 4 см.
Сравнить полученные результаты с теми, которые будут, если предположить, что индукция по всему сечению сердечника неизменна и равна индукции, соответствующей осевой линии.
Указание. Найти напряженность магнитного поля в любой точке сечения сердечника, пользуясь законом полного тока.
Ответ:
Задача 6. Прямолинейный проводник, длина которого равна 40 см, перемещается со скоростью 25 м/сек под углом α = 30° к линиям однородного магнитного поля, имеющего магнитную индукцию, равную 1 Вб/м2. Определить величину ЭДС, индуктированной в проводнике.
Ответ: 5 В.
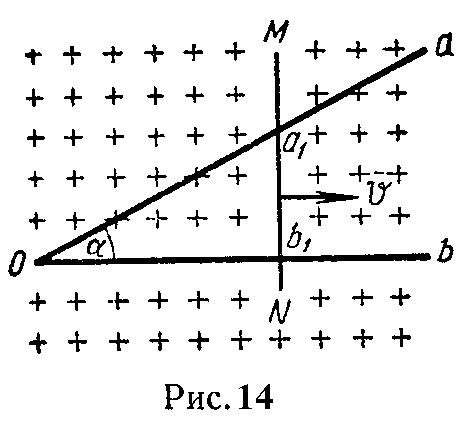
Задача 7. В однородном магнитном поле, индукция которого B, находится проволока aOb, изогнутая под углом α, по которой скользит проводник MN с равномерной скоростью v (рис. 14).
Вектор магнитной индукции перпендикулярен плоскости угла aOb. Все проводники обладают сопротивлением r0 на единицу длины. Найти выражения для наводимой ЭДС и тока, протекающего в контуре a1Ob1.
Решение
Обозначим отрезок a1b1 через h, а переменный отрезок Ob1 — через x.
Площадь треугольника a1Ob1 равна
Магнитный поток, пронизывающий контур треугольника,
Имея в виду, что dx/dt = v, по формуле (19) найдем выражение для наводимой ЭДС
ЭДС растет пропорционально x, ибо этой величине пропорциональна активная часть a1b1 перемещающегося проводника MN.
Сопротивление контура проводника a1Ob1a1
Заметим, что величина сопротивления также возрастает пропорционально расстоянию x.
Искомый ток
т.е. по контуру протекает постоянный ток.
Задача 8. В однородном магнитном поле, индукция которого В = 0,5 Вб/м2, вокруг оси О вращается с равномерной скоростью прямоугольная рамка (рис. 15). Построить кривые изменения магнитного потока, пронизывающего рамку и наводимой в рамке ЭДС в функции времени. Рамка делает 1500 об/мин, ее размеры: a = 10 см, b = 20 см.
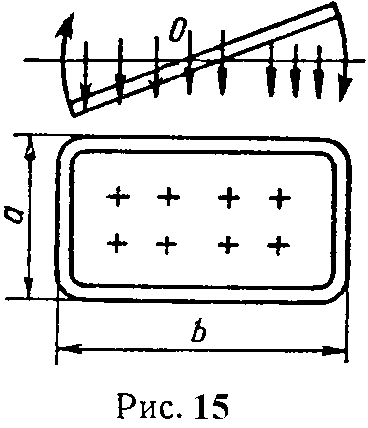
Как изменятся частота и величина максимальной ЭДС, наведенной в рамке, если: а) индукцию увеличить в 2 раза, б) сторону a увеличить в 2 раза, в) скорость вращения увеличить в 2 раза.
Ответ: Ф = 0,01cos50πt Вб, e = 1,57sin50πt В; а) и б) частота не изменится, Em увеличится в 2 раза; в) частота и Em увеличатся в 2 раза.
Задача 9. Круглый виток, радиус которого равен 5 см, находится в однородном магнитном поле, перпендикулярном плоскости витка, и изменяется с течением времени по уравнению В = Вmsinωt. Построить кривые изменения во времени магнитного потока, пронизывающего виток и наводимой в нем ЭДС, если Вm = 8000 Гс и ω = 628 1/с.
Единица индукции магнитного поля в системе единиц СИ Тесла (Тл), а в системе единиц СГСМ Гаусс (Гс). Соотношение между единицами: 1 Тл = 10000 Гс.
Ответ: Ф = 6,28·10–3sinωt Вб, e = –3,95cosωt В.
Задача 10. Построить кривую ЭДС, наводимой магнитным потоком в катушке, имеющей w =100 витков. Поток в функции времени изменяется согласно рис. 16, а, б, в, г.
Во всех случаях Фm = 10–2 Вб. Данные кривых:
Решение
а) Наводимая ЭДС определяется по формуле (19).
На первом участке в интервале времени от нуля до t1 поток возрастает; за время dt происходит положительное приращение потока dФ (рис. 16, д). Вследствие линейного характера кривой отношение dФ/dt есть величина постоянная.
Величина наводимой ЭДС будет равна
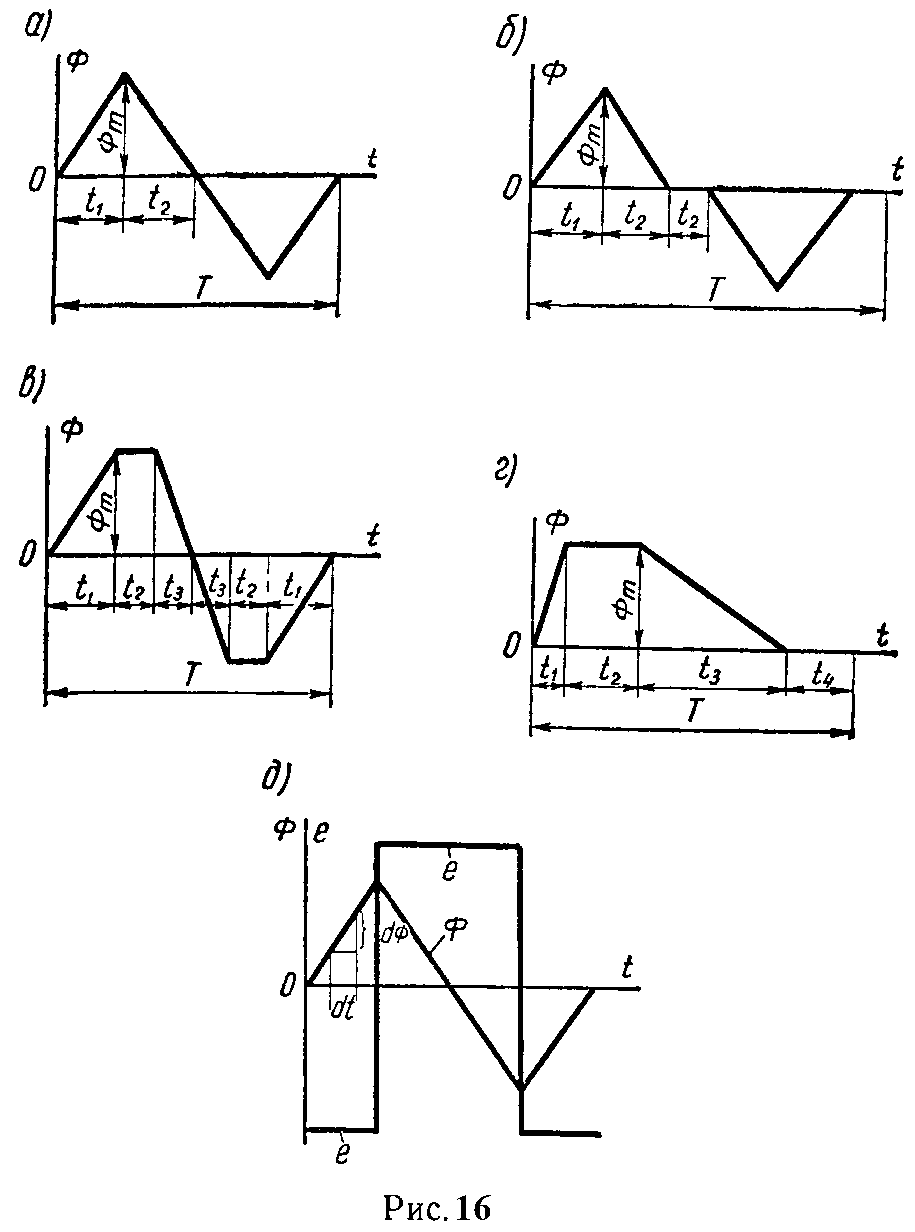
На втором участке t2 происходит спад кривой потока по прямой линии и, следовательно, dФ/dt также есть величина постоянная, но имеющая отрицательный знак; за время dt поток получает отрицательное приращение (dФ < 0); наводимая ЭДС равна
На третьем участке за время dt поток продолжает убывать; и dФ/dt есть величина отрицательная; наводимая ЭДС равна +200 В; на четвертом участке магнитный поток возрастает с той же скоростью, что и на первом участке; наводимая ЭДС равна –200 В.
На рис. 16, д начерчена кривая наводимой ЭДС.
Задача 11. В центре цилиндрической катушки длиною l = 30 см и диаметром D = 10 см, состоящей из w = 400 витков, помещен виток, ось которого совпадает с осью катушки (рис. 17).
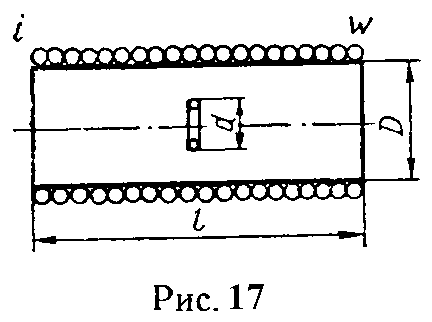
По катушке проходит ток
i = Imsinωt (Im = 4 А, ω = 314 с–1).
Определить взаимную индуктивность катушки и витка и ЭДС, наводимую в витке, если диаметр витка d = 0,5 см.
Ввиду малости размеров витка по сравнению с размерами катушки при расчете принять, что магнитная индукция, определяемая током в катушке во всех точках, лежащих в плоскости витка, будет такой же, как и в центре витка.
Полагая, что виток, перпендикулярный к оси цилиндрической катушки, расположен на расстоянии x от ее центра, построить кривую зависимости взаимной индуктивности катушки и витка в функции x.
Для построения кривой подсчет произвести для различных точек при изменении x от нуля до +l (соседние значения x брать через каждые 5 см).
Ответ: M = 31,2·10–9 Гн = 31,2 нГн; e = –39,2cos314t мкВ.
|
x, см |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
M, нГн |
31,2 |
30,7 |
26,3 |
16,1 |
4,63 |
1,62 |
0,72 |
Задача 12. Катушка прямоугольной формы, средние размеры сторон которой равны a = 8 см, b = 15 см, содержащая w = 20 витков тонкой проволоки, находится в плоскости проводов двухпроводной линии передачи энергии, по которой проходит ток I = 100 А (рис. 18).
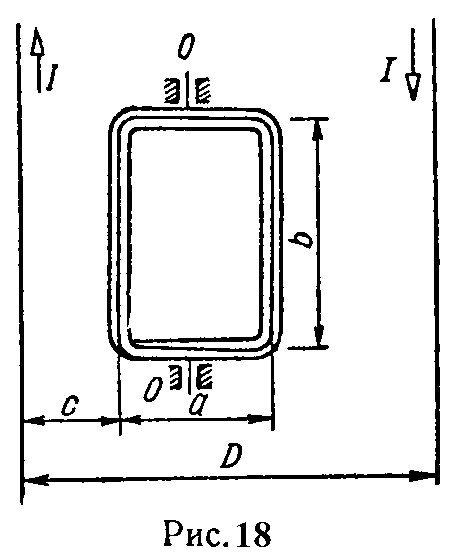
Расстояние между осью левого провода и серединой ближайшей стороны катушки c = 2 см. Расстояние между проводами линии D = 20 см.
Чему равна энергия потока взаимной индукции линии и катушки? Какова сила, действующая на катушку, если по ней проходит ток I = 0,5 А? Определить количество индуктированного в рамке электричества при ее повороте вокруг оси OO на 180°, если сопротивление катушки r = 0,08 Ом.
Примечание. Следует иметь в виду, что энергия потока взаимной индукции
где Ф — магнитный поток, пронизывающий катушку, а I — ток в линии, определяющий этот поток.
Ответ: 6,6 мДж; 0,109 Гн; 33·10–4 Кл.
Задача 13. Определить индуктивность катушки, если известно, что при прохождении через нее синусоидального тока i = Imsinωt амплитуда (максимальная величина) наведенной ЭДС самоиндукции равна Em.
Дано Im = 2 А; ω = 5000 с–1; Em = 200 В.
Решение
По формуле (23) находим выражение для мгновенной величины электродвижущей силы самоиндукции, наводимой в катушке,
Коэффициент при cosωt является амплитудой ЭДС самоиндукции, наведенной в катушке, т.е.
откуда
Задача 14. Определить индуктивность цилиндрической катушки без стального сердечника, имеющей w витков, длину l и сечение S. Расчет провести при следующих данных: a) w1 = 300, l1 = 60 см, S1 = 1 см2; б) w2 = 200, l2 = 60 см, S2 = 10 см2.
Решение
Индуктивность катушки вычисляем по формуле (25) с учетом коэффициента k, являющегося функцией отношения диаметра катушки к ее длине; значения k приведены в таблице 1.
а) Диаметр катушки найдем из формулы
затем определяем коэффициент k1
Так как k1 >50, то индуктивность находим по формуле (24)
б) Найдем D2 и k2
По таблице 1 находим, что отношению D/l = 0 соответствует k = 1, а отношению D/l = 0,1 соответствует k = 0,9588; путем интерполирования находим k, соответствующее отношению D2/l2 = 0,0595.
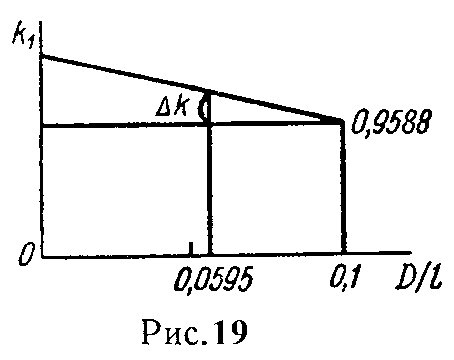
Из рис. 19 определяем
откуда Δk = 0,0167, следовательно,
k = 0,9588 + Δk = 0,9588 + 0,0167 = 0,9755,
по формуле (25) находим индуктивность
Задача 15. Индуктивность короткой цилиндрической катушки (для которой D:l = 1), имеющей 500 витков, равна 0,01 Гн. Определить индуктивность катушки, имеющей то же число витков и такую же длину, но у которой отношение D:l = 0,4.
Ответ: 2 мГн.
Задача 16. Определить индуктивность катушки, состоящей из 400 витков, намотанной на кольцевой сердечник, изготовленный из листовой электротехнической стали Э11, если ток I = 1 А. Сердечник имеет квадратное сечение. Радиусы: R1 = 3 см, R2 = 4 см.
Чему будет равна индуктивность, если в тороиде сделать зазор δ = 0,5 мм (рис. 20).
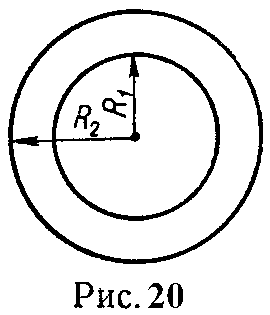
Указание. Надо рассчитать магнитную цепь, а для определения L воспользоваться формулой (21).
Ответ: 57,4 мГн; 32,8 мГн.
Задача 17. Катушка из 600 витков навита на стальной тороид, поперечное сечение которого равно 40 см2. Индуктивность катушки равна L1 = 2,5 Гн. Чему равна длина воздушного промежутка, который необходимо сделать в сердечнике для уменьшения индуктивности до 2 Гн?
При решении задачи принять, что магнитная проницаемость сердечника постоянна и очень велика по сравнению с единицей.
Решение
Магнитное сопротивление катушки без зазора
Для уменьшения индуктивности катушки в 1,25 раза ее магнитное сопротивление должно увеличиться в 1,25 раза, т. е. положив сечение пути потока в воздухе равным с сечением сердечника, получим
где δ — длина воздушного зазора, отсюда
Индуктивность катушки, определяемая по формуле (24), равна
отсюда
Сравнивая два выражения для отношения l к µr, получим
Отсюда рассчитывается необходимая длина воздушного зазора
Задача 18. На сердечник, изготовленный из листовой электротехнической стали Э11, имеющий регулируемый воздушный зазор, намотана катушка. Когда воздушный промежуток уменьшен до нуля, индуктивность катушки равна 3,5 Гн. При каком воздушном зазоре индуктивность катушки будет равна 2,5 Гн, если при зазоре в 1 мм ее индуктивность равна 2 Гн?
Принять, что абсолютная магнитная проницаемость сердечника постоянна.
Ответ: 0,53 мм.
Задача 19. Определить индуктивность 1 км воздушной медной двухпроводной линии, радиус проводов которой равен 2 мм и расстояние между осями проводов равно 30 см.
Ответ: 2 мГн.
Задача 20. Определить индуктивность 1 км воздушной медной однопроводной линии, радиус провода которой равен 2,5 мм. Расстояние провода от земли 5 м.
Ответ: 1,656 мГн.
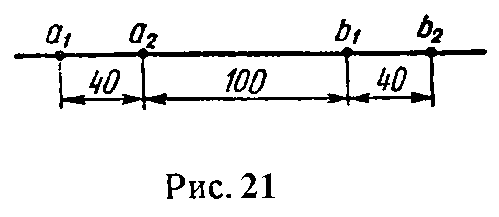
Задача 21. Найти взаимную индуктивность на 1 км между двумя параллельными линиями a1a2 и b1b2 (рис. 21). Радиусы проводов считать малыми по сравнению с расстояниями между их осями, заданными на рис. 21.
Решение
Расчет взаимной индуктивности проведем по формуле (32). Чтобы ею воспользоваться найдем расстояния: от оси первого провода первой линии до оси первого провода второй линии
r11 = a1b1 = 140 см;
от оси первого провода первой линии до оси второго провода второй линии
r12 = a1b2 = 180 см;
от оси второго провода первой линии до оси первого провода второй линии
r21 = a2b1 = 100 см;
и, наконец, от оси второго провода первой линии до оси второго провода второй линии
r22 = a2b2 = 140 см.
Искомая взаимная индуктивность
Задача 22. Четыре длинных прямых параллельных провода расположены в вершинах квадрата (рис. 22).
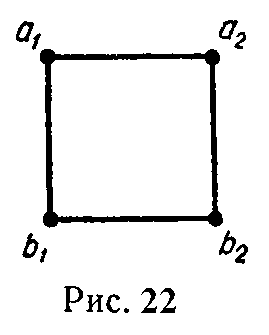
Провода a1a2 образуют одну цепь, провода b1b2 — другую. Чему равна взаимная индуктивность этих цепей на 1 км, если сторона квадрата равна 20 см? Радиусы проводов считать достаточно малыми (например, 1,5–2 мм).
Ответ: 0,1386 мГн.
Задача 23. Найти взаимную индуктивность двух катушек, изображенных на рис. 23.
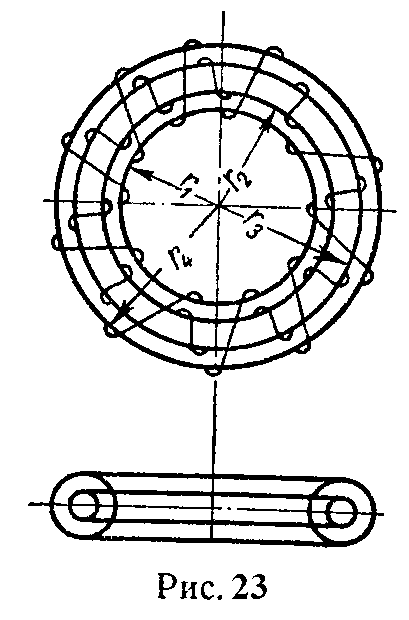
Число витков наружной катушки w1 = 200, число витков внутренней катушки w2 = 500; r1 = 8 см, r2 = 10 см, r3 = 12 см, r4= 14 см.
Решение
Взаимная индуктивность определяется по формуле (31), в которой под S надо понимать ту площадь, которая пронизывается потоком, сцепленным как с током первой так и с током второй катушки, т.е. площадь сечения меньшей катушки S2 равна
Полагая распределение магнитной индукции равномерным по сечениям обеих катушек, найдем
Задача 24. Под линией электропередачи Л1Л2 подвешены бронзовые провода линии связи a1a2 (рис. 24).
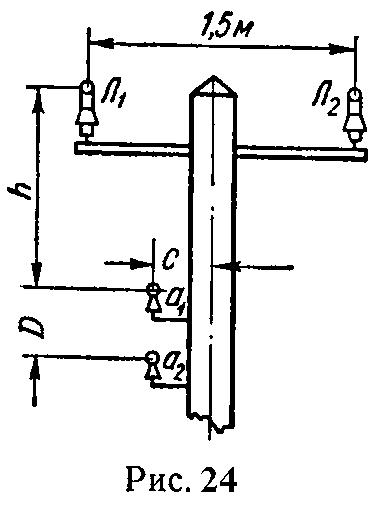
Определить индуктивность одного километра линии a1a2, диаметр проводов которой d = 3 мм, а расстояние между осями проводов D = 30 см.
Чему равна взаимная индуктивность на 1 км длины между линиями Л1Л2 и a1a2, если расстояния равны: h = 100 см, c = 25 см.
Какая электродвижущая сила наводится в линии связи, если по линии электропередачи протекает ток
i = Imsinωt,
где Im = 600 А, ω = 314 с–1.
Ответ: L = 2,12 мГн, M = 14 мкГн; e = –2,54cosωt В.
Задача 25. Определить взаимную индуктивность двух круговых витков, имеющих общую ось (рис. 25).
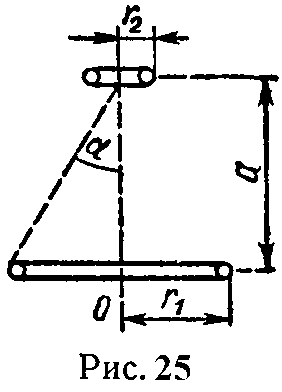
Радиусы витков r1 = 4 см, r2 = 0,5 см. Принять, что напряженность магнитного поля, определяемая током в большем витке во всех точках, лежащих в плоскости второго витка (внутри его), будет такой же, как и в центре второго витка.
Задачу решить для двух случаев: а) a = 0, б) a = 3 см.
На какое расстояние от центра 0 надо удалить второй виток, чтобы взаимная индуктивность составляла 1% от взаимной индуктивности в случае, когда плоскости витков совпадают.
Указание. Положив, что по большему витку проходит ток I, надо вычислить напряженность магнитного поля, созданную этим током в центре меньшего витка; умножив найденное значение H на магнитную постоянную и площадь, ограниченную меньшим витком, найти величину магнитного потока, пронизывающего этот виток. Разделив этот поток на ток I, получают искомую взаимную индуктивность (формула 29).
Ответ: а) 1,23 нГн; б) 0,63 нГн, 18,2 см.
Задача 26. На кольцо, изготовленное из литой стали, средний диаметр которого равен 25 см, навиты две катушки. Радиус поперечного сечения кольца 2 см. В первой катушке 250 витков, во второй — 500 витков. Относительную магнитную проницаемость стали принять постоянной и равной 1000. Определить индуктивность каждой катушки и их взаимную индуктивность (полагая распределение магнитной индукции в сечении кольца равномерным).
Ответ: L1 = 125,6 мГн; L2 = 502,4 мГн; M = 251,2 мГн.
Задача 27. Цилиндрическая катушка длиною в 1 м и диаметром в 10 см имеет 1000 витков. Вторая катушка, поперечное сечение которой 0,5 см2, а длина 1 см, имеет 10 витков. Катушки расположены так, что их оси совпадают.
Принять, что магнитная индукция, определяемая током первой катушки во всех точках, лежащих внутри второй катушки, будет такой же, как и в центре второй катушки. Определить взаимную индуктивность катушек, в случаях: а) когда их центры совпадают, б) когда центр второй катушки расположен на одном из концов первой катушки, в) когда их центры удалены друг от друга на 60 см.
Ответ: а) 0,625 мкГн; б) 0,314 мкГн; в) 0,033 мкГн.
Задача 28. Определить взаимную индуктивность двух катушек, индуктивности которых 0,04 и 0,16 Гн, а коэффициент связи равен 0,75.
Ответ: M = 0,06 Гн.
Задача 29. Определить коэффициент рассеяния двух катушек, индуктивности которых 30 и 120 мГн, а взаимная индуктивность равна 0.03 Гн.
Ответ: σ = 0,75.
Задача 30. Определить энергию магнитного поля цилиндрической катушки, содержащей 500 витков. Длина катушки равна 10 см. диаметр равен тоже 10 см; по виткам катушки проходит ток в 2 А. Среда — воздух.
Указание. Сначала следует вычислить индуктивность катушки по формуле (25), а затем энергию магнитного поля по формуле (36).
Ответ: 0,034 Дж.
Задача 31. Чему равна энергия магнитного поля катушки, имеющей 1000 витков и индуктивность которой равна 2 мГн, если магнитный поток, определяемый проходящим по катушке током, равен 2·10–5 Вб.
Ответ: 0,1 Дж.
Задача 32. Исходя из выражения интеграла магнитной энергии
определить полную индуктивность коаксиального кабеля длиною l = 1 км, радиус внутреннего проводника которого r1 = 2 мм, внутренний радиус внешнего проводника r2 = 7,2 мм, внешний радиус внешнего проводника r3 = 7,5 мм (рис. 26).
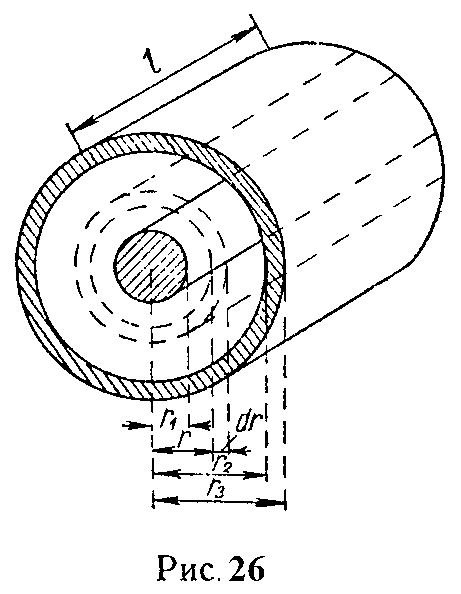
Относительную магнитную проницаемость материала внутреннего и внешнего проводника, а также пространства между проводниками принять равной 1.
Определить энергию магнитного поля на 1 м длины кабеля, запасаемую во внутреннем проводе, между проводом и трубой и внутри трубы, если I = 1 А.
Указание. Индуктивность следует определить из выражения
которое следует применить по отдельности к области внутри внутреннего проводника, к полости трубы и к области внешнего проводника. При расчете энергии каждый раз надо рассматривать малый трубчатообразный объем (рис. 26)
dV = 2πr·dr·l.
Значение напряженности поля в каждой из областей было найдено в задаче 1.
В результате решения должно быть получено для внутренней индуктивности внутреннего проводника L' = 0,05 мГн, то же для внешнего проводника L" = 0,0045 мГн, и для внешней индуктивности Lвне = 0,256 мГн. Полная индуктивность
L = L' + L" + Lвне = 0,31 мГн.
Искомую энергию следует определять по формуле (36).
Задача 33. По двум катушкам, индуктивности которых равны L1 = 0,5 Гн, L2 = 1 Гн, а их взаимная индуктивность составляет M = 0,5 Гн, проходят токи I1 = 6 А, I2 = 4 А. Определить полную магнитную энергию этой системы.
Ответ: 29 Дж.
 удельная энергия магнитного поля,
энергия магнитного поля,
коэффициент магнитной связи,
взаимная индуктивность,
индуктивность однопроводной линии,
индуктивность двухпроводной линии,
индуктивность соленоида,
ЭДС самоиндукции,
индуктивность,
закон электромагнитной индукции,
второй закон Кирхгофа для магнитных цепей,
первый закон Кирхгофа для магнитных цепей,
сила Ампера,
закон Ампера,
сила Лоренца,
закон полного тока,
магнитная постоянная,
закон Био Савара Лапласа
удельная энергия магнитного поля,
энергия магнитного поля,
коэффициент магнитной связи,
взаимная индуктивность,
индуктивность однопроводной линии,
индуктивность двухпроводной линии,
индуктивность соленоида,
ЭДС самоиндукции,
индуктивность,
закон электромагнитной индукции,
второй закон Кирхгофа для магнитных цепей,
первый закон Кирхгофа для магнитных цепей,
сила Ампера,
закон Ампера,
сила Лоренца,
закон полного тока,
магнитная постоянная,
закон Био Савара Лапласа
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
